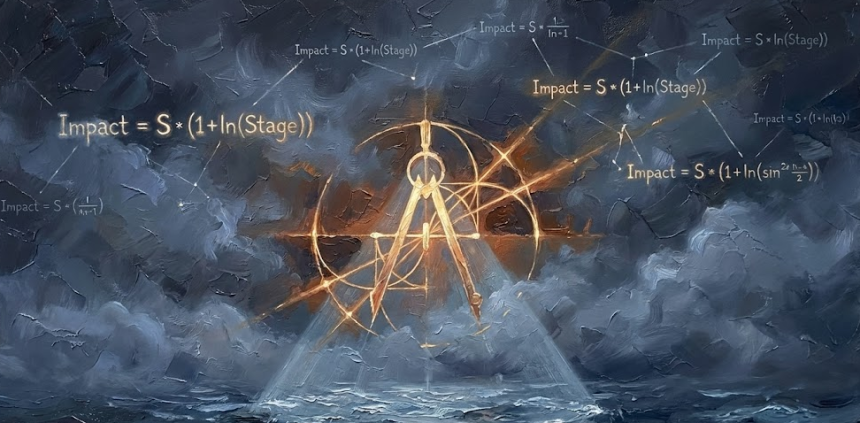If Part 1 discussed the elegance of ‘Conjugate Priors’ and ‘Analytical Solutions’—the heart of the Bayesian engine—Part 2 examines how we mathematically conquer the most menacing phantom in the business field: ‘Silence.’
This post goes beyond simple sales management; it delves into the inner workings of how Information Theory and Statistical Weighting Design combine to visualize risks hidden within the fog of uncertainty.
The frontlines of actual business, particularly in Sales or SCM (Supply Chain Management), are not places where data flows like a mighty river as described in textbooks.
Rather, they are spaces filled with scarcity, disconnection, and ‘Silence.’ Trainable (big) data is often scarce, representatives are too busy and frequently miss inputs, and systems are often left neglected for days.
Today, in Part 2, we explore the aesthetic design of the Exa engine (based on Normalized Sequential Bayesian Inference: NSBI), which translates even this ‘vacuum of data’ into mathematical risk. Borrowing from Alan Turing’s statistical intuition and Information Theory, we unveil the mathematical foundation of “a system that works without data and becomes smarter the longer it remains silent.”
1. The Time Function of Entropy: Silence is Not ‘Zero’
The most dangerous moment in business is not when bad news arrives. Rather, it is when the “period of no news” drags on. Ignoring or neglecting this silence inevitably leads to critical errors in judgment.
1.1 “Time Kills All Deals”: The Increase of Entropy
From the perspective of Information Theory, the fact that no new information is flowing in over time is, in itself, powerful evidence that the system’s Entropy (disorder/uncertainty) is increasing. The adage “No news is good news” rarely applies in business. Time Kills All Deals.
Our model does not treat this ‘time of silence’ as a simple void. Instead, it calculates risk through a mathematical logic known as ‘Time Decay.’
1.2 Mathematical Implementation: Expansion of Uncertainty (Variance)
In the field, if a record is not updated within a defined period, the engine subtly increases the (beta, failure parameter) value of the Bayesian distribution as time passes. Mathematically, this is an act of forcibly widening the Variance of the probability distribution.
This is defined by the following formula:
Where (lambda) is the Risk Sensitivity (Decay Factor), and s the duration of silence.
- Interpretation: Even if the probability of winning a deal was a solid 80% yesterday, if a day (or a set period) passes today without any interaction, the system will self-corrode that confidence by tomorrow morning. This is a warning sent by the system. It mathematically implements the business truth that “Confidence decays when left unattended.” The model flattens the probability curve, interpreting silence not as ‘maintenance of the status quo’ but as the ‘erosion of trust.’
2. The Geometry of Weight: The Weber-Fechner Law
Does the exact same “positive signal”—for example, a decision-making executive attending a meeting—carry the same weight in all situations? Meeting a decision-maker at the first introduction (Stage 1) versus meeting them just before the final contract (Stage 5) are vastly different scenarios; the latter is far more decisive and carries greater impact.
How can we mathematically control this subtle ‘context of the situation’? Simply increasing the weight linearly (1x, 2x, 3x) is dangerous. It risks making the system too simplistic or causing it to fluctuate wildly by reacting too sensitively in later stages.
2.1 Logarithmic Weighting
To address this, we apply the ‘Weber-Fechner Law’ from cognitive psychology to our model. The principle states that “human sensory perception relates to stimulus intensity in a logarithmic function.” It is valid to reflect the importance of business stages not as an exponential explosion, but as a heavy, steady increase following a logarithmic curve.
The formula for Stage Weight () reflecting this is as follows:
Here, ‘Stage’ is a value defined according to the negotiation steps specific to the individual corporate environment.
According to this formula, the weight for Stage 1 (Discovery) is , while the weight for Stage 5 (Negotiation) becomes approximately . In other words, a single signal at the final stage is processed as a ‘decisive blow’ that is 2.6 times more powerful than one at the beginning. This result mathematically implements the field tension of “It ain’t over till it’s over” within a framework of stability.
3. Paving a Way Where There is No Data: Heuristic Modeling
Cases where “sufficient past data (especially unstructured data) exists for training” are relatively rare in corporate environments. However, the model shines even in these situations. The strength of Bayesian inference lies in its ability to enable ‘rational inference’ even in the absence of data.
Instead of forcing the learning of incomplete data, we choose ‘Heuristic Scoring,’ which transplants the intuition of veteran experts into the model.
3.1 Heuristic Score Table
During World War II, Alan Turing succeeded in cracking the German Enigma code by gathering small fragments of information. He focused on the ‘Quality of Information’ rather than quantity, establishing the concept of Weight of Evidence (WoE).
Our model inherits this philosophy, compressing tens of thousands of situations occurring in the business field into key signals and quantifying their ‘information density’ through an expert’s lens. The ‘Heuristic Score Table’ is not statistic; it is a Definition reflecting field experience and prior knowledge. While it can be standardized depending on the uniqueness of the field, the idea can be briefly defined as follows:
- Strong Affirmation Signal: Clear signs of success, such as budget confirmation or executive attendance.
- Active Resistance Signal: Shadows of failure, such as mentioning competitors or delaying schedules.
- Game Changer Signal: Powerful events capable of flipping the entire probability with a single signal, such as verbal approval.
Each Stage and Signal is assigned a unique score value. The table defining these is not the result of big data analysis, but rather the wisdom of the field—“If the decision-maker participates, it is twice as certain as when a working-level staffer does”—fixed as a constant ().
4. The Heart of the Engine: The Marriage of Intuition and Mathematics (Likelihood)
Now, let us look at how these elements interlock within the calculation process at the heart of the Bayesian engine (Exa).
The moment a user inputs a meeting stage (Stage X) and a signal captured from the meeting result (Signal Y) into the system (via Mobile, Tablet, Laptop, etc.), the Update Formula is activated.
Expanding this into the overall Impact Formula, the final shock value calculated by the system is derived as follows:
This process corresponds to calculating the evidence data (Likelihood) examined in Part 1, which combines with the Prior Distribution to update the Posterior Probability.
Conclusion: Weight Hidden in Lightness
Paradoxically, the core of Part 2 lies in the ‘Lightness of the System.’
Without expensive GPU servers or multi-year data purification projects, we can create the most realistic inference engine for enterprise environments by combining field experience, practical knowledge, and human intuition—crystallized in just two tables (Stage Log Weights, Signal Heuristic Scores) and mathematical principles.
- The Time Decay Formula wakes us from lazy optimism.
- The Impact Formula prevents rash judgments and captures decisive moments.
- Expert Heuristics fill the void of data and silence with wisdom.
We do not build magic in a black box; we build our house on explainable, rigorous mathematical logic.
[Next Up: Part 3]
In the next session, we will address the final puzzle that transforms cold statistical probability (Raw Probability) into hot business decision-making: ‘Decision Calibration and the Aesthetics of the Sigmoid Function.’