BA02.[부록3] 영업성공확률 의사결정시스템

의사결정 임피던스 매칭(Decision Impedance Matching)

BA02.[Exa 베이지안 추론] 영업의 보이지 않는 손: 60일의 도박 에피소드의 지난 제1부와 제2부를 통해 우리는 베이지안 엔진이 어떻게 ‘사전 믿음’을 세우고, ‘시그널’과 ‘침묵’을 통해 확률의 궤적을 추적하는지 살펴보았다. 이제 우리 손에는 베이지안 파라미터 α와 β에 의해 정교하게 계산된 순수 사후확률 P_raw가 들려 있다.

하지만 아직 끊나지 않았다. 마지막 의사결정 과정이 남아있기 때문이다. 60%의 확률이라도, 그것이 단 한 번의 미팅으로 얻은 것인지, 아니면 수십 번의 협상 끝에 도출된 것인지에 따라 결단의 무게는 완전히 다를 수 있다.

안타깝게도 인간의 뇌는 선형적인 숫자만으로 움직이지 않는다. 오늘 부록 3부에서는 베이지안 파라미터가 가진 ‘증거의 총량’을 통해 냉정한 확률을 결단의 언어로 바꾸는 ‘의사결정 임피던스 매칭(Decision Impedance Matching)’의 비밀을 탐구해 본다.

---

1. 숫자의 늪: 왜 51%는 결단하기에 부족한가?

수학적으로 51%는 절반을 넘었으므로 ‘성공 가능성이 높음’을 의미한다. 하지만 비즈니스의 사생결단 현장에서 51%는 사실상 ‘모 아니면 도’인 도박과 다름없다.

비즈니스 현장에서 가장 위험한 것은 ‘근거 없는 낙관’이다.

• 상황 A: $\alpha=0.6, \beta=0.4 \implies P = 60\%$
• 상황 B: $\alpha=60, \beta=40 \implies P = 60\%$

수학적 확률(P)은 둘 다 60%이다. 하지만 리더의 입장에서 상황 A는 ‘운에 맡겨야 하는 도박’이고, 상황 B는 수많은 검증을 거친 결과(A와 B의 α, β 크기가 다르다. 즉, 믿음의 크기가 다른 것이다)이다. 전자는 바람 한 점에도 0%나 100%로 널뛰기 할 수 있는 불안정한 상태이지만, 후자는 웬만한 악재에도 흔들리지 않는 ‘관성’을 가진 상태이다.

인간의 뇌는 단순히 ‘비율’만 보지 않는다. 그 뒤에 깔린 ‘증거의 두께’를 직관적으로 계산한다. 우리는 이 직관을 시스템의 로직으로 명시화할 필요가 있다.

인간은 불확실성을 혐오하며, 특정 ‘임계점(Threshold)’을 넘기 전까지는 행동을 유보하는 본성을 가지고 있다. 반대로 한 번 확신이 서면, 85%의 확률이나 95%의 확률이나 똑같이 ‘확실함’으로 받아들인다.

이처럼 ‘수학적 확률’과 ‘심리적 확신’ 사이에는 거대한 간극이 존재한다. 전자공학에서 서로 다른 두 회로를 연결할 때 에너지 손실을 줄이기 위해 저항값을 맞추는 것을 ‘임피던스 매칭’이라 하듯, 시스템의 숫자와 인간의 결단력을 연결하는 정교한 조율이 필요하다.

---

2. 증거의 총량($n$): 의사결정의 임계 질량

BA02 에피소드에서 적용된 Exa의 엔진은, 베이지안 사후확률(여기서는 P_raw로 표현)과 증거의 총량($n = \alpha + \beta$)을 의사결정의 필터로 사용한다. 이것이 바로 ‘의사결정 임피던스 매칭’의 핵심이다.

2.1 신뢰의 부피와 정보 밀도

베이지안 파라미터 α와 β는 각각 ‘성공의 증거’와 ‘실패의 증거’가 쌓인 무게이다. 이 둘의 합인 $n$은 이 딜에 대해 우리가 ‘얼마나 많이 알고 있는가’를 나타내는 지표가 된다.

• n이 작을 때 (에너지 불일치): 시스템의 확률이 아무리 높아도 리더의 확신으로 이어지지 않는다. 위험하기 때문이다. 이는 회로의 임피던스가 맞지 않아 에너지가 전달되지 않는 상태이다. 이때 엔진은 확률 대신 “데이터 부족(Not Enough Evidence)”이라는 경고를 보낸다.
• n이 클 때 (임피던스 매칭): 확률 숫자가 리더의 결단력과 공명하기 시작한다. 충분한 증거가 쌓였으므로, 이제 확률 1%의 변화는 실제 비즈니스 리스크의 1% 변화로 정교하게 전달된다.

이에 엔진은 조직의 축적된 총체적 지식을 담아서 인간의 인지 구조와 유사한 ‘시그모이드 함수’를 통과시켜 숫자를 다시 빚어낸다.

2.2 시그모이드 보정: 확률에 ‘의지’를 담는다

우리는 다음과 같은 비선형성을 통해 확률의 밀도를 조정한다.

$$P_{calibrated} = \frac{1}{1 + e^{-k(P_{raw} – P_{0})}}$$

여기서 $P_{raw}$는 엔진이 계산한 베이지안의 원천 사후확률이며, $k$는 확신의 기울기(확신의 강도), $P_0$ 는 의사결정의 임계점이다.

• 완만한 구간 (불확실성): 확률이 30~50% 사이일 때는 보정값이 매우 보수적으로 움직인다. “아직은 믿지 마라”는 신호다.
• 가파른 구간 (결단): 확률이 60%를 넘어서는 순간, 시그모이드 곡선은 가파르게 올라간다. 작은 긍정적 시그널 하나가 확률을 60%에서 80%로 상승시킨다.
• 포화 구간 (확신): 85%를 넘어서면 곡선은 다시 완만해진다. 90%나 95%나 인간에게는 동일한 ‘Commit’ 상태임을 반영하는 것이다.

지금부터 의사결정 임피던스 매칭에 사용되는 핵심 개념 로그오즈(Log-odds)를 오버뷰하고 엔진 내부를 수학적으로 파헤쳐 본 뒤, 마지막으로 비즈니스 시뮬레이션을 통해 이를 이해해 보자.

---

3. 숨겨진 세계: 로그 오즈(Log-odds)의 축적

Exa의 베이지안 업데이트가 일어나는 엔진 내부를 들여다보면, 확률은 우리가 아는 0~100%의 모습이 아니다. 베이지안의 파라미터 α, β는 수학적으로 ‘로그 오즈(Log-odds)’라는 무한한 선형 공간에서 작동한다.

$$logit(P) = \ln\left(\frac{P}{1-P}\right) = \ln\left(\frac{\alpha}{\beta}\right)$$

우리가 영업 미팅과정에서 새로운 시그널을 얻을 때마다, 시스템은 이 로그 오즈 값을 정직하게 더해 나간다.

• 협상과정에서 포착한 성공 시그널은 $+ \Delta \alpha$를 통해 값을 밀어 올리고,
• 실패 시그널과 시간 감쇠($\lambda$)는 $+ \Delta \beta$를 통해 값을 끌어내린다.

이 과정은 전기 회로에서 전하가 축적되는 과정과 같다. 하지만 이 에너지는 아직 ‘회로 내부의 전압’일 뿐으로 이를 실제 기기를 돌리는 ‘동력’으로 바꾸려면 외부 저항과 맞물리는 인터페이스가 필요하다.

3.1. 시그모이드 확률로의 매핑

왜 하필 시그모이드 함수일까? 그것은 시그모이드가 바로 위 로그 오즈 함수의 역함수(Inverse Function)이기 때문이다. 무한한 범위($-\infty \sim +\infty$)에서 쌓인 증거의 합을 우리가 이해할 수 있는 0.0 ~ 1.0 사이의 확률 세계로 돌려보내는 수학적 유일해이다.

$$P = \frac{1}{1 + e^{-k(x – x_0)}}$$

여기서 $x$는 우리가 쌓아온 로그 오즈($\ln\frac{\alpha}{\beta}$)이다. 이 수식은 단순히 숫자를 예쁘게 만드는 것이 아니라, 무한한 정보의 에너지를 유한한 의사결정의 범위로 압축하는 장치이다.

3.2 확률의 세계 vs 정보의 세계

우리가 사는 세상은 ‘확률(Probability)’로 대화하지만, 데이터가 쌓이는 원리는 ‘정보의 축적(Information Accumulation)‘이다.

• 확률의 세계 ($0 \sim 1$): 이 세계는 매우 좁고 답답하다. 0.9에서 0.99로 가기는 어렵고, 1.0이라는 벽에 막혀 있다. 여기서 숫자를 더하거나 빼면 금방 벽에 부딪힌다. (예: $0.9 + 0.2 = 1.1 \to$불가능)
• 정보의 세계 ($-\infty \sim +\infty$): 이 세계는 끝이 없다. 증거가 쌓이면 쌓일수록 숫자는 무한히 커질 수 있고, 반대 증거가 나오면 무한히 작아질 수 있다.

로그오즈(Log-odds)는 바로 이 좁은 확률의 세계를 광활한 정보의 세계로 펼쳐놓은 지도이다.

3.3 왜 로그오즈가 더 합당하고 설득력이 있는가

① 증거의 ‘더하기’ 가능 (Additivity)

베이지안 업데이트의 핵심은 새로운 정보가 들어올 때마다 확률을 수정하는 것이다. 확률 공간에서는 이를 위해 복잡한 곱셈과 나눗셈을 반복해야 하지만, 로그오즈 공간에서는 단순한 덧셈이 된다.

오늘 미팅이 좋았다(+2 점), 하지만 경쟁사가 나타났다(-1.5 점)

이렇게 우리가 직관적으로 점수를 매기고 더할 수 있는 이유는 우리 뇌가 이미 내부적으로 로그오즈와 유사한 선형적인 계산을 하고 있기 때문이다.

② 0과 1이라는 ‘벽’ 제거

확률이 99.9%일 때와 $99.99$일 때, 우리는 둘 다 “거의 확실하다”고 느끼지만 그 사이에는 엄청난 양의 추가 증거가 필요하다. 로그오즈는 $1$에 가까워질수록 숫자를 기하급수적으로 크게 펼쳐줌으로써, 확신이 깊어질수록 더 많은 증거가 필요하다는 비즈니스적 진실을 정확히 묘사한다.

③ 대칭성 (Symmetry)

성공 확률이 $80\%$인 상황과 실패 확률이 $80\%$인 상황(성공$20\%$)은 동전의 양면과 같다. 로그오즈 공간에서는 이 두 상황이 $+1.38$과 -1.38로 나타난다. 즉, 긍정과 부정의 에너지가 거울처럼 완벽한 대칭을 이루게 되어 로직의 일관성이 확보된다.

3.4 베이지안 파라미터와의 연결

$\alpha$와 $\beta$를 사용하여 로그오즈($L$)를 표현하면 다음과 같다.

$$L = \ln\left(\frac{\alpha}{\beta}\right)$$

• 성공 증거(α)가 많아지면 $L$은 양수(+)로 커진다.
• 실패 증거(β)가 많아지면 $L$은 음수(-)로 작아진다.
• 둘의 무게가 같으면 $L$은 $0$이 된다. (확률 $50\%$)

이처럼 로그오즈는 “누구의 목소리가 더 큰가?”를 결정하는 저울의 눈금과 같다. 여기까지가 로그오즈가 왜 ‘확률을 무한한 정보 공간으로 펼쳐서 선형적으로 계산’하는 개념인지 그리고 비즈니스 로직에서 “더 합당한 근거”가 되는지에 대한 큰 그림이다.

---

4. 수학적 전개

좀 더 궁금한 독자들을 위해 Exa의 엔진에서 수학적으로 어떻게 베이지안의 파라미터($\alpha, \beta$)가 로그오즈라는 통로를 거쳐 시그모이드 함수의 지수 부분에 안착하게 되는지, 그 과정을 단계별로 보이고자 한다. 읽는 이에 따라 이 부분이 가장 흥미로운 시간이 될 수도 있겠다.

4.1 출발점: 베이지안 사후 확률 ($P$)

먼저, 우리가 업데이트한 주인공 α와 β를 이용해 계산된 순수 확률 $P$를 정의_{[부록1, 2]}한다.

$$P = \frac{\alpha}{\alpha + \beta}$$

이 P값은 0과 1 사이를 움직이며, 우리가 직관적으로 이해하는 (사후)확률 즉, 승률이다.

4.2 로그오즈(Log-odds)로의 변환

이제 이 확률을 무한한 정보 공간인 로그오즈($x$)로 펼친다. 로그오즈의 정의에 따라 수식을 전개하면 놀라운 결과가 나온다.

$$x = \ln\left(\frac{P}{1-P}\right)$$

여기에 위에서 정의한 $P$값을 대입해 보겠다.

$$x = \ln\left(\frac{\frac{\alpha}{\alpha + \beta}}{1 – \frac{\alpha}{\alpha + \beta}}\right) = \ln\left(\frac{\frac{\alpha}{\alpha + \beta}}{\frac{\beta}{\alpha + \beta}}\right) = \ln\left(\frac{\alpha}{\beta}\right)$$

즉, 로그오즈 $x$는 단순히 성공 증거($\alpha$)와 실패 증거($\beta$)의 비율에 로그를 취한 값이 된다. 이것이 정보의 세계에서 우리가 쌓은 ‘순수한 증거의 무게‘이다.

오즈($Odds$): BA01.[The Short Shot] 수학해설 참고.

4.3 의사결정 임계점 ($T$)의 변환

의사결정의 임계점 $T$ 역시 확률 단위(0.8 등)이다. 이를 로그오즈 공간의 기준점인 $x_0$로 변환한다.

$$x_0 = \ln\left(\frac{T}{1-T}\right)$$

이제 우리는 모든 데이터를 ‘로그오즈’라는 동일한 척도 위에서 비교할 준비가 되었다.

4.4 최종 시그모이드 결합 (임피던스 매칭)

이제 마지막으로 시그모이드 함수의 지수 부분에 이 모든 값을 집어넣는다. 시그모이드 함수는 지수 부분에 ‘현재의 에너지($x$)와 기준 에너지($x_0$)의 차이’를 받아들인다.

$$P_{out} = \frac{1}{1 + e^{-k(x – x_0)}}$$

이 식에 위에서 구한 $x$와 $x_0$를 대입하여 지수 부분($-k(x – x_0)$)을 정리해 보자.

$$-k \left( \ln\frac{\alpha}{\beta} – \ln\frac{T}{1-T} \right) = -k \ln\left( \frac{\alpha / \beta}{T / (1-T)} \right)$$

따라서 최종 수식은 다음과 같이 변모한다.

$$P_{out} = \frac{1}{1 + \left( \frac{\beta \cdot T}{\alpha(1-T)} \right)^k}$$

4.5 수학적 결론과 비즈니스적 의미

이 전개가 왜 ‘임계 질량’과 ‘설득력’을 증명하는지 요약해 보자.

1. 지수의 마법: 지수 부분에 있던 복잡한 $e$와 $ln$이 만나 서로 상쇄되면서, 결과적으로 성공 비율($\alpha/\beta$)과 목표 비율($T/1-T$)의 상대적 크기만 남게 된다.
2. $k$의 위력: $k$가 지수 자리에 위치하게 되면서, 성공 증거가 목표치를 조금만 넘어서도 확률을 가파르게 증가시킨다.
3. 데이터의 무게 반영: 단순히 확률($P$)만 보는 것이 아니라, $\alpha와 \beta$라는 증거의 절대량이 커질수록 이 비율의 힘이 더 견고해진다.

---

5. 비즈니스 시뮬레이션

실제 비즈니스 시나리오를 통해 이 수학적 모델이 어떻게 ‘결단의 에너지’를 만들어내는지 증명해 보이자.

어느 조직의 성향에 맞춰 마스터 기준 값을 다음과 같이 설정한다고 하자.

• 의사결정 임계점 ($T$):0.7 (70%)
  • 해석: “최소한 70%의 확률적 근거는 있어야 승부를 걸어볼 만하다.”
• 결단 가속도 ($k$):10
  • 해석: “임계점을 넘어서면 공격적으로 한다”

최종 수식:

$$P_{out} = \frac{1}{1 + \left( \frac{\beta \cdot T}{\alpha(1-T)} \right)^k}$$

5.1 시뮬레이션 비즈니스 시나리오

이제 초기의 믿음(사전분포)이 순차적으로 업데이트 된 사후분포를 갖는 영업 협상 과정의 어느 단계를 생각한다. 아래의 $\alpha와 \beta$는 지금까지 협상 과정의 Stage와 Signal로부터 베이지안 엔진에서 업데이트 되어온 $\alpha$, $\beta$의 값이다.

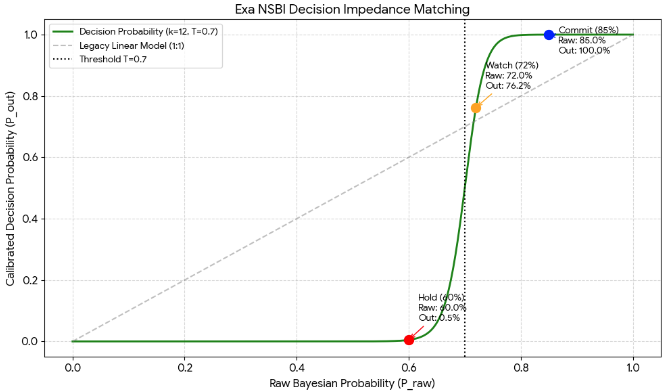
상황 1: 임계점 미달 (긴가민가한 상태)

• 데이터: $\alpha = 6.0, \beta = 4.0 (순수 확률 P_{raw} = 60\%)$
• 계산 과정:
  1. 비율 계산: $\frac{4.0 \cdot 0.7}{6.0 \cdot 0.3} = \frac{2.8}{1.8} \approx 1.55$
  2. $k$승 적용: $1.55^{10} \approx 81.3$
  3. 최종: $P_{out} = \frac{1}{1 + 81.3} \approx$1.2%
• 해석: 베이지안 확률은 60% 이지만, 조직의 기준 $P_{out}$이 (70%)에 못 미친다. 시스템은 결단 에너지를 차단하여 의사결정권을 갖은 자에게 “아직은 절대 믿지 마라(Hold)”는 억제 신호를 보낸다.

상황 2: 임계점 돌파 (결단의 시작)

• 데이터: $\alpha = 7.2, \beta = 2.8 (순수 확률 P_{raw} = 72\%)$
• 계산 과정:
  1. 비율 계산: $\frac{2.8 \cdot 0.7}{7.2 \cdot 0.3} = \frac{1.96}{2.16} \approx 0.907$
  2. $k$승 적용: $0.907^{10} \approx 0.38$
  3. 최종 확률: $P_{out} = \frac{1}{1 + 0.38} \approx$ 72.4%
• 해석: 확률이 임계점(T=0.7)을 살짝 넘어서자, 억제되었던 에너지가 풀리며 순수 확률이 그대로 대시보드에 반영되기 시작한다. “이제부터 관심을 두고 지켜볼 가치가 있다(Watch)”는 신호이다.

상황 3: 임계 질량 돌파 (확신단계 진입)

• 데이터: $\alpha = 8.5, \beta = 1.5 (순수 확률 P_{raw} = 85\%)$
• 계산 과정:
  1. 비율 계산: $\frac{1.5 \cdot 0.7}{8.5 \cdot 0.3} = \frac{1.05}{2.55} \approx 0.411$
  2. k승 적용: $0.411^{10} \approx 0.0001$
  3. 최종 확률: $P_{out} = \frac{1}{1 + 0.0001} \approx$ 99.9%
• 해석: 확률이 85%에 도달하자 가속도 $k$가 마법을 부린다. 시스템은 85%라는 숫자를 “이 프로젝트는 되는 사업이다”라는 99.9%의 확신(Commit)으로 밀어 올린다. 리더는 더 이상 주저할 이유가 없다.

5.2 Insight

시나리오 각 상황을 요약해서 비교해 보자.

상태	순수 확률 (Praw​)	보정 확률 (Pout​)	의사결정 등급	비즈니스 액션
미달	60%	1.2%	Hold	자원 투입 엄격 금지
돌파	72%	72.4%	Push	전략적 집중 시작
폭발	85%	99.9%	Commit	전사적 자원 집중

Insight: 왜 이 모델이 승리하는가: 영업 의사결정의 시스템화

1. 희망 고문의 제거: 60% 확률을 가진 딜들을 과감히 1%로 바닥에 깔아버림으로써, 영업 현장의 고질적인 병폐인 ‘근거 없는 낙관‘을 시스템이 원천 차단한다. 그럼에도 60%의 사후확률은 중요하다. 따라서 엔진은 베이지안 확률과 의사결정 보정확률을 대시보드에 같이 display해야 한다.
2. 병목 자원의 집중: 72%와 85%는 단 13%의 차이일 뿐이지만, 시스템은 이를 ‘관심’과 ‘확신’이라는 전혀 다른 차원으로 분리해 낸다. 덕분에 경영진은 어느 사업에 내 시간을 쏟아야 하는지를 본능적으로 알게 된다.
3. 임피던스 매칭의 실체: 이 비선형적인 도약이야말로 베테랑 리더들이 현장에서 느끼는 “감(感)이 왔다!”는 심리적 상태를 수학적으로 완벽하게 복제한 것이다.
   
   
   

베이지안 엔진이 강력함은 로직 자체 뿐 아니라, 그것을 조직의 전략, 성격에 맞게 튜닝할 수 있는 유연성(Flexibility)에 있다.