Phối hợp Trở kháng Ra quyết định (Decision Impedance Matching)

Thông qua Phần 1 và Phần 2 của tập BA02 [Suy luận Bayesian Exa] “Bàn tay vô hình của kinh doanh: Canh bạc 60 ngày” vừa qua, chúng ta đã xem xét cách Động cơ Bayesian thiết lập ‘Niềm tin tiên nghiệm’ và theo dõi quỹ đạo của xác suất thông qua ‘Tín hiệu’ và ‘Sự im lặng’. Giờ đây, trong tay chúng ta là xác suất hậu nghiệm thuần túy P_raw được tính toán tinh vi bởi các tham số Bayesian α và β.

Nhưng vẫn chưa kết thúc. Bởi vì quy trình ra quyết định cuối cùng vẫn còn đó. Ngay cả với xác suất 60%, trọng lượng của quyết định có thể hoàn toàn khác nhau tùy thuộc vào việc nó có được từ một cuộc họp duy nhất hay được rút ra sau hàng chục cuộc đàm phán.

Thật không may, bộ não con người không chỉ hoạt động dựa trên những con số tuyến tính. Trong Phụ lục Phần 3 hôm nay, chúng ta sẽ khám phá bí mật của ‘Phối hợp Trở kháng Ra quyết định (Decision Impedance Matching)’, thứ biến xác suất lạnh lùng thành ngôn ngữ của sự quyết đoán thông qua ‘tổng lượng bằng chứng’ mà các tham số Bayesian nắm giữ.

1. Vũng lầy của những con số: Tại sao 51% là chưa đủ để quyết định?

Về mặt toán học, 51% là hơn một nửa nên nó có nghĩa là ‘khả năng thành công cao’. Nhưng tại hiện trường sinh tử của kinh doanh, 51% thực tế không khác gì một canh bạc ‘được ăn cả ngã về không’.

Điều nguy hiểm nhất tại hiện trường kinh doanh là ‘sự lạc quan vô căn cứ’.

• Tình huống A: α=0.6, β=0.4 (P=60%)
• Tình huống B: α=60, β=40 (P=60%)

Xác suất toán học (P) đều là 60%. Nhưng ở vị trí của người lãnh đạo, Tình huống A là ‘canh bạc phải phó mặc cho may mắn’, còn Tình huống B là kết quả trải qua vô số kiểm chứng (Kích thước α, β của A và B khác nhau. Tức là, độ lớn của niềm tin là khác nhau). Trường hợp trước là trạng thái bất ổn có thể nhảy vọt lên 0% hoặc 100% chỉ với một cơn gió nhẹ, còn trường hợp sau là trạng thái có ‘quán tính’ không dễ bị lung lay bởi những tin xấu thông thường.

Bộ não con người không chỉ nhìn vào ‘tỷ lệ’. Nó tính toán theo trực giác ‘độ dày của bằng chứng’ nằm bên dưới đó. Chúng ta cần minh định hóa trực giác này thành logic của hệ thống.

Con người ghét sự không chắc chắn và có bản năng trì hoãn hành động cho đến khi vượt qua một ‘Ngưỡng (Threshold)’ nhất định. Ngược lại, một khi đã chắc chắn, họ chấp nhận xác suất 85% hay 95% đều giống nhau là ‘sự chắc chắn’.

Như vậy, tồn tại một khoảng cách khổng lồ giữa ‘xác suất toán học’ và ‘sự chắc chắn tâm lý’. Giống như trong kỹ thuật điện tử, khi kết nối hai mạch khác nhau, người ta thực hiện ‘phối hợp trở kháng’ để giảm thiểu tổn thất năng lượng, cần có sự điều chỉnh tinh vi kết nối các con số của hệ thống với năng lực quyết đoán của con người.

2. Tổng lượng bằng chứng (n): Khối lượng tới hạn của việc ra quyết định

Động cơ Exa được áp dụng trong tập BA02 sử dụng xác suất hậu nghiệm Bayesian (ở đây biểu thị là P_raw) và tổng lượng bằng chứng (n = α + β) làm bộ lọc ra quyết định. Đây chính là cốt lõi của ‘Phối hợp Trở kháng Ra quyết định’.

2.1 Thể tích của niềm tin và Mật độ thông tin

Các tham số Bayesian α và β lần lượt là trọng lượng tích lũy của ‘bằng chứng thành công’ và ‘bằng chứng thất bại’. Tổng của cả hai, n, trở thành chỉ số biểu thị chúng ta ‘biết bao nhiêu’ về thương vụ này.

• Khi n nhỏ (Bất đồng năng lượng): Dù xác suất của hệ thống có cao đến đâu cũng không dẫn đến sự chắc chắn của lãnh đạo. Vì nó nguy hiểm. Đây là trạng thái năng lượng không được truyền tải do trở kháng của mạch không khớp. Lúc này, động cơ gửi đi cảnh báo “Thiếu dữ liệu (Not Enough Evidence)” thay vì xác suất.
• Khi n lớn (Phối hợp trở kháng): Con số xác suất bắt đầu cộng hưởng với sự quyết đoán của lãnh đạo. Vì bằng chứng đầy đủ đã tích lũy, giờ đây thay đổi 1% xác suất được truyền tải chính xác thành thay đổi 1% rủi ro kinh doanh thực tế.

Theo đó, động cơ chứa đựng kiến thức tổng thể được tích lũy của tổ chức và nhào nặn lại con số bằng cách cho nó đi qua ‘Hàm Sigmoid’ tương tự như cấu trúc nhận thức của con người.

2.2 Hiệu chỉnh Sigmoid: Đưa ‘Ý chí’ vào xác suất

Chúng ta điều chỉnh mật độ của xác suất thông qua tính phi tuyến tính sau đây.

$$P_{calibrated} = \frac{1}{1 + e^{-k(P_{raw} – P_{0})}}$$

Ở đây $P_{raw}$ là xác suất hậu nghiệm nguồn Bayesian do động cơ tính toán, k là độ dốc của sự chắc chắn (cường độ chắc chắn), $P_0$ là điểm ngưỡng ra quyết định.

• Vùng thoải (Không chắc chắn): Khi xác suất nằm trong khoảng 30~50%, giá trị hiệu chỉnh di chuyển rất bảo thủ. Là tín hiệu “Đừng tin vội”.
• Vùng dốc (Quyết đoán): Khoảnh khắc xác suất vượt quá 60%, đường cong Sigmoid đi lên dốc đứng. Một tín hiệu tích cực nhỏ nâng xác suất từ 60% lên 80%.
• Vùng bão hòa (Chắc chắn): Nếu vượt quá 85%, đường cong lại trở nên thoải. Nó phản ánh rằng 90% hay 95% đối với con người đều là trạng thái ‘Commit’ giống nhau.

Từ bây giờ, hãy tổng quan về khái niệm cốt lõi Log-odds được sử dụng trong phối hợp trở kháng ra quyết định và đào sâu vào bên trong động cơ về mặt toán học, sau đó cuối cùng hãy hiểu điều này thông qua mô phỏng kinh doanh.

3. Thế giới ẩn giấu: Sự tích lũy của Log-odds

Nhìn vào bên trong động cơ nơi xảy ra cập nhật Bayesian của Exa, xác suất không có hình dạng 0~100% mà chúng ta biết. Các tham số Bayesian α, β hoạt động về mặt toán học trong không gian tuyến tính vô hạn gọi là ‘Log-odds’.

$$logit(P) = \ln\left(\frac{P}{1-P}\right) = \ln\left(\frac{\alpha}{\beta}\right)$$

Mỗi khi chúng ta thu được tín hiệu mới trong quá trình họp kinh doanh, hệ thống sẽ cộng giá trị Log-odds này một cách trung thực.

• Tín hiệu thành công bắt được trong quá trình đàm phán đẩy giá trị lên thông qua +Δα.
• Tín hiệu thất bại và suy giảm theo thời gian (λ) kéo giá trị xuống thông qua +Δβ.

Quá trình này giống như quá trình tích tụ điện tích trong mạch điện. Nhưng năng lượng này vẫn chỉ là ‘điện áp bên trong mạch’, để biến nó thành ‘động lực’ vận hành thiết bị thực tế, cần có giao diện ăn khớp với điện trở bên ngoài.

3.1 Ánh xạ sang xác suất Sigmoid

Tại sao lại cứ phải là hàm Sigmoid? Đó là vì Sigmoid chính là Hàm ngược (Inverse Function) của hàm Log-odds ở trên. Là lời giải toán học duy nhất trả tổng bằng chứng tích lũy trong phạm vi vô hạn (-∞ ~ +∞) về thế giới xác suất từ 0.0 ~ 1.0 mà chúng ta có thể hiểu được.

$$P = \frac{1}{1 + e^{-k(x – x_0)}}$$

Ở đây x là Log-odds (ln(α/β)) mà chúng ta đã tích lũy. Công thức này không đơn thuần là thiết bị làm đẹp con số, mà là thiết bị nén năng lượng thông tin vô hạn vào phạm vi ra quyết định hữu hạn.

3.2 Thế giới của Xác suất vs Thế giới của Thông tin

Thế giới chúng ta sống đối thoại bằng ‘Xác suất (Probability)’, nhưng nguyên lý tích lũy dữ liệu là ‘Tích lũy thông tin (Information Accumulation)’.

• Thế giới của Xác suất (0 ~ 1): Thế giới này rất hẹp và ngột ngạt. Khó đi từ 0.9 đến 0.99, và bị chặn bởi bức tường 1.0. Tại đây nếu cộng hoặc trừ con số thì sẽ sớm va phải tường. (Ví dụ: 0.9 + 0.2 = 1.1 → Không thể)
• Thế giới của Thông tin (-∞ ~ +∞): Thế giới này không có kết thúc. Bằng chứng càng tích lũy thì con số càng có thể lớn vô hạn, và nếu bằng chứng ngược lại xuất hiện thì có thể nhỏ vô hạn.

Log-odds chính là tấm bản đồ mở rộng thế giới xác suất chật hẹp này ra thế giới thông tin rộng lớn.

3.3 Tại sao Log-odds hợp lý và thuyết phục hơn

① Khả năng ‘cộng’ bằng chứng (Additivity)

Cốt lõi của cập nhật Bayesian là sửa đổi xác suất mỗi khi thông tin mới đi vào. Trong không gian xác suất, để làm điều này phải lặp lại các phép nhân và chia phức tạp, nhưng trong không gian Log-odds, nó trở thành phép cộng đơn giản.

“Cuộc họp hôm nay tốt (+2 điểm), nhưng đối thủ cạnh tranh đã xuất hiện (-1.5 điểm)”

Lý do chúng ta có thể chấm điểm và cộng lại theo trực giác như thế này là vì bộ não của chúng ta đã thực hiện các phép tính tuyến tính tương tự như Log-odds bên trong.

② Loại bỏ ‘bức tường’ 0 và 1

Khi xác suất là 99.9% và 99.99999%, chúng ta đều cảm thấy “gần như chắc chắn”, nhưng giữa chúng cần một lượng bằng chứng bổ sung khổng lồ. Log-odds mô tả chính xác sự thật kinh doanh rằng “sự chắc chắn càng sâu sắc thì càng cần nhiều bằng chứng” bằng cách mở rộng con số theo cấp số nhân khi nó tiến gần đến 1.

③ Tính đối xứng (Symmetry)

Tình huống xác suất thành công là 80% và tình huống xác suất thất bại là 80% (thành công 20%) giống như hai mặt của đồng xu. Trong không gian Log-odds, hai tình huống này xuất hiện dưới dạng +1.38 và -1.38. Tức là, năng lượng tích cực và tiêu cực tạo thành sự đối xứng hoàn hảo như tấm gương, đảm bảo tính nhất quán của logic.

3.4 Kết nối với tham số Bayesian

Biểu diễn Log-odds (L) sử dụng α và β như sau:

$$L = \ln\left(\frac{\alpha}{\beta}\right)$$

• Nếu bằng chứng thành công (α) nhiều lên thì L lớn lên theo số dương (+).
• Nếu bằng chứng thất bại (β) nhiều lên thì L nhỏ đi theo số âm (-).
• Nếu trọng lượng của cả hai bằng nhau thì L trở thành 0. (Xác suất 50%)

Như vậy Log-odds giống như vạch chia của cái cân quyết định “Giọng nói của ai to hơn?”. Đến đây là bức tranh lớn về việc tại sao Log-odds là khái niệm ‘mở rộng xác suất ra không gian thông tin vô hạn để tính toán tuyến tính’ và trở thành “căn cứ hợp lý hơn” trong logic kinh doanh.

4. Triển khai toán học

Để phục vụ độc giả tò mò hơn, tôi muốn hiển thị từng bước quá trình làm thế nào các tham số Bayesian (α, β) trong động cơ Exa đi qua con đường Log-odds và an tọa tại phần số mũ của hàm Sigmoid về mặt toán học. Tùy thuộc vào người đọc, phần này có thể là thời gian thú vị nhất.

4.1 Điểm xuất phát: Xác suất hậu nghiệm Bayesian (P)

Trước tiên, xác định xác suất thuần túy P được tính toán bằng cách sử dụng nhân vật chính α và β mà chúng ta đã cập nhật.

$$P = \frac{\alpha}{\alpha + \beta}$$

Giá trị P này di chuyển giữa 0 và 1, và là xác suất (hậu nghiệm) mà chúng ta hiểu theo trực giác, tức là tỷ lệ thắng.

4.2 Chuyển đổi sang Log-odds

Bây giờ, mở rộng xác suất này ra không gian thông tin vô hạn là Log-odds (x). Triển khai công thức theo định nghĩa của Log-odds sẽ cho ra kết quả đáng kinh ngạc.

$$x = \ln\left(\frac{P}{1-P}\right)$$

Hãy thử thay thế giá trị P đã định nghĩa ở trên vào đây.

$$x = \ln\left(\frac{\frac{\alpha}{\alpha + \beta}}{1 – \frac{\alpha}{\alpha + \beta}}\right) = \ln\left(\frac{\frac{\alpha}{\alpha + \beta}}{\frac{\beta}{\alpha + \beta}}\right) = \ln\left(\frac{\alpha}{\beta}\right)$$

Tức là, Log-odds x đơn giản trở thành giá trị lấy log của tỷ lệ bằng chứng thành công (α) và bằng chứng thất bại (β). Đây là ‘trọng lượng bằng chứng thuần túy’ mà chúng ta đã tích lũy trong thế giới thông tin.

4.3 Chuyển đổi ngưỡng ra quyết định (T)

Ngưỡng ra quyết định T cũng là đơn vị xác suất (0.8 v.v.). Chuyển đổi cái này thành x_0, điểm chuẩn trong không gian Log-odds.

$$x_0 = \ln\left(\frac{T}{1-T}\right)$$

Giờ đây chúng ta đã sẵn sàng so sánh tất cả dữ liệu trên cùng một thước đo gọi là ‘Log-odds’.

4.4 Kết hợp Sigmoid cuối cùng (Phối hợp trở kháng)

Bây giờ cuối cùng đưa tất cả các giá trị này vào phần số mũ của hàm Sigmoid. Hàm Sigmoid chấp nhận ‘sự chênh lệch giữa năng lượng hiện tại (x) và năng lượng chuẩn (x_0)’ vào phần số mũ.

$$P_{out} = \frac{1}{1 + e^{-k(x – x_0)}}$$

Hãy thay thế x và x_0 đã tìm được ở trên vào công thức này và sắp xếp phần số mũ.

$$-k \left( \ln\frac{\alpha}{\beta} – \ln\frac{T}{1-T} \right) = -k \ln\left( \frac{\alpha / \beta}{T / (1-T)} \right)$$

Do đó công thức cuối cùng biến đổi như sau.

$$P_{out} = \frac{1}{1 + \left( \frac{\beta \cdot T}{\alpha(1-T)} \right)^k}$$

4.5 Kết luận toán học và ý nghĩa kinh doanh

Hãy tóm tắt tại sao sự triển khai này chứng minh ‘khối lượng tới hạn’ và ‘sức thuyết phục’.

1. Phép màu của số mũ: e và ln phức tạp ở phần số mũ gặp nhau và triệt tiêu lẫn nhau, kết quả là chỉ còn lại độ lớn tương đối của tỷ lệ thành công (α/β) và tỷ lệ mục tiêu (T/(1-T)).
2. Uy lực của k: Khi k nằm ở vị trí số mũ, chỉ cần bằng chứng thành công vượt qua giá trị mục tiêu một chút thôi cũng làm tăng xác suất một cách dốc đứng.
3. Phản ánh trọng lượng dữ liệu: Không chỉ nhìn đơn thuần vào xác suất (P), mà lượng tuyệt đối của bằng chứng gọi là α và β càng lớn thì sức mạnh của tỷ lệ này càng trở nên vững chắc.

5. Mô phỏng kinh doanh

Hãy chứng minh mô hình toán học này tạo ra ‘Năng lượng của sự quyết đoán’ như thế nào thông qua kịch bản kinh doanh thực tế.

Giả sử chúng ta thiết lập giá trị chuẩn master phù hợp với khuynh hướng của một tổ chức nào đó như sau.

• Ngưỡng ra quyết định (T): 0.7 (70%)
  • Diễn giải: “Ít nhất phải có căn cứ xác suất 70% thì mới đáng để thử đánh cược.”
• Gia tốc quyết đoán (k): 10
  • Diễn giải: “Nếu vượt qua điểm ngưỡng thì hành động quyết liệt.”
• Công thức cuối cùng:$$P_{out} = \frac{1}{1 + \left( \frac{\beta \cdot T}{\alpha(1-T)} \right)^k}$$

5.1 Kịch bản kinh doanh mô phỏng

Bây giờ, hãy nghĩ về một giai đoạn nào đó của quá trình đàm phán kinh doanh có phân phối hậu nghiệm được cập nhật tuần tự từ niềm tin ban đầu (phân phối tiên nghiệm). α và β dưới đây là giá trị của α, β đã được cập nhật trong động cơ Bayesian từ Stage và Signal của quá trình đàm phán cho đến nay.

Tình huống 1: Chưa đạt ngưỡng (Trạng thái bán tín bán nghi)

• Dữ liệu: α=6.0, β=4.0 (Xác suất thuần túy P_raw = 60%)
• Quá trình tính toán:
  • Tính tỷ lệ: (4.0 * 0.7) / (6.0 * 0.3) ≈ 1.55
  • Áp dụng lũy thừa k: 1.55^10 ≈ 81.3
  • Cuối cùng: P_out = 1 / (1 + 81.3) ≈ 1.2%
• Diễn giải: Xác suất Bayesian là 60%, nhưng không đạt chuẩn P_out (70%) của tổ chức. Hệ thống chặn năng lượng quyết đoán và gửi tín hiệu ức chế “Vẫn chưa được tin tuyệt đối (Hold)” cho người nắm quyền ra quyết định.

Tình huống 2: Đột phá ngưỡng (Bắt đầu quyết đoán)

• Dữ liệu: α=7.2, β=2.8 (Xác suất thuần túy P_raw = 72%)
• Quá trình tính toán:
  • Tính tỷ lệ: (2.8 * 0.7) / (7.2 * 0.3) ≈ 0.907
  • Áp dụng lũy thừa k: 0.907^10 ≈ 0.38
  • Xác suất cuối cùng: P_out = 1 / (1 + 0.38) ≈ 72.4%
• Diễn giải: Ngay khi xác suất vượt nhẹ qua điểm ngưỡng (T=0.7), năng lượng bị kìm nén được giải phóng và xác suất thuần túy bắt đầu được phản ánh nguyên vẹn lên bảng điều khiển. Là tín hiệu “Từ bây giờ đáng để quan tâm theo dõi (Watch)”.

Tình huống 3: Đột phá khối lượng tới hạn (Tiến vào giai đoạn chắc chắn)

• Dữ liệu: α=8.5, β=1.5 (Xác suất thuần túy P_raw = 85%)
• Quá trình tính toán:
  • Tính tỷ lệ: (1.5 * 0.7) / (8.5 * 0.3) ≈ 0.411
  • Áp dụng lũy thừa k: 0.411^10 ≈ 0.0001
  • Xác suất cuối cùng: P_out = 1 / (1 + 0.0001) ≈ 99.9%
• Diễn giải: Ngay khi xác suất đạt 85%, gia tốc k làm phép. Hệ thống đẩy con số 85% lên thành sự chắc chắn 99.9% (Commit) rằng “Dự án này là thương vụ thành công”. Lãnh đạo không còn lý do gì để do dự nữa.

5.2 Insight

Hãy tóm tắt và so sánh từng tình huống kịch bản.

Trạng thái	Xác suất thuần túy (P_raw)	Xác suất hiệu chỉnh (P_out)	Cấp độ ra quyết định	Hành động kinh doanh
Chưa đạt	60%	1.2%	Hold	Nghiêm cấm đầu tư nguồn lực
Đột phá	72%	72.4%	Push	Bắt đầu tập trung chiến lược
Bùng nổ	85%	99.9%	Commit	Tập trung nguồn lực toàn công ty

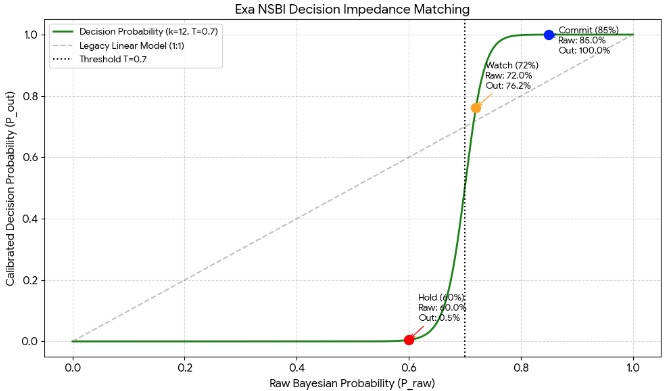
Insight: Tại sao mô hình này chiến thắng – Hệ thống hóa ra quyết định kinh doanh

1. Loại bỏ hy vọng hão huyền: Bằng cách mạnh dạn dìm các thương vụ có xác suất 60% xuống đáy 1%, hệ thống chặn đứng tận gốc ‘sự lạc quan vô căn cứ’, căn bệnh mãn tính của hiện trường kinh doanh. Mặc dù vậy, xác suất hậu nghiệm 60% vẫn quan trọng. Do đó động cơ phải hiển thị cùng lúc xác suất Bayesian và xác suất hiệu chỉnh ra quyết định trên bảng điều khiển.
2. Tập trung nguồn lực nút thắt cổ chai: 72% và 85% chỉ chênh lệch 13%, nhưng hệ thống tách chúng ra thành các chiều kích hoàn toàn khác nhau là ‘Quan tâm’ và ‘Chắc chắn’. Nhờ đó ban lãnh đạo biết được theo bản năng mình phải đổ thời gian vào công việc kinh doanh nào.
3. Thực thể của phối hợp trở kháng: Cú nhảy vọt phi tuyến tính này chính là sự sao chép toán học hoàn hảo trạng thái tâm lý “Có linh cảm rồi!” mà các lãnh đạo kỳ cựu cảm thấy tại hiện trường.

Sức mạnh của Động cơ Bayesian không chỉ nằm ở bản thân logic, mà còn ở Tính linh hoạt (Flexibility) có thể tinh chỉnh nó cho phù hợp với chiến lược, tính cách của tổ chức.