本文是旨在查明以小说形式连载的“BA03 On-Time 资材入库:Bayesian MCMC”篇中活跃的 EXA 引擎运作原理的技术解说系列的第一篇文章。
本系列涵盖了贝叶斯推断中属于高级技术的混合分布 (Mixture Distribution) 和 MCMC (Markov Chain Monte Carlo) Gibbs Sampling,因此内容较深,计算过程可能会有些复杂。因此,为了尽可能容易地消化这些内容,我们打算分阶段详细探讨,预计这将是一段相当漫长的旅程。
为了理解整体脉络,建议您先阅读小说原文。此外,由于贝叶斯理论是分阶段扩展概念的,如果您先查阅 BA01 及 BA02 的剧集和数学解说,将对接受本次内容有很大帮助。因为之前的数学概念和逻辑是延续下来的。
1. 数据的定义:观测偏差 (Observation Deviation)
为了对小说中探讨的核心议题“On-Time (准时到达)”进行数学建模,我们首先必须定义数据。为此,生成如下以天 (Day) 为单位的样本观测数据:
$$D = [d_1, d_2, \dots, d_7] = \{ -2, -1, 0, 1, 2, 0, 9 \}$$
我们可以将这组观测到的延迟天数集合 视为一个向量 (Vector),其中包含的每个延迟值 (-2, -1, 0 …) 成为构成该向量的元素 (Element,或成分)。
在这里,个别数据元素 $d_i$ 定义如下:
$$d_i = (\text{实际日期}) – (\text{计划日期})$$
这个公式的含义非常直观。
- : 准确遵守约定的情况 (On-Time)
- : 比计划延迟的情况 (例如:+5 表示延迟 5 天)
- : 比计划提前到达的情况 (早期入库)
这种延迟天数 (Delay Days) 模型可以应用于测量商业现场的各种瓶颈 (Bottleneck)。
- 资材入库及供应商的作业延迟 (Lead Time Delay)
- 运输及物流延迟 (Transportation Delay)
- 生产线的工序延迟 (Production Delay)
向量数据的大小(维度)取决于业务规模。如果观测到的交易业绩是 100 笔,它将是由 100 个元素组成的向量;如果是 300 笔,它将是由 300 个元素组成的向量。
在本系列中,为了明确剖析 EXA 引擎的运作原理,使用上述定义的 7 个“玩具数据 (Toy Data)”作为示例。虽然数百、数千条数据是现实的,但在直观地展示复杂的计算过程方面存在局限性。
当然,在实际应用到现场时,必须根据“供应商+品目+运输手段+目的地”或生产的“产线+产品”等决策目的对数据进行细分 (Granularity) 管理,通过这一点可以准确捕捉 SCM 全盘的风险。
2. 数据的可视化:两个峰值
好了,现在让我们来可视化我们的 Toy Data (向量 )。确认一下 7 个元素在图表上是如何分布的。
现实的数据如何呢? 下面是用直方图表示的某企业 200 笔实际资材采购交易业绩(特定供应商的特定品目)。
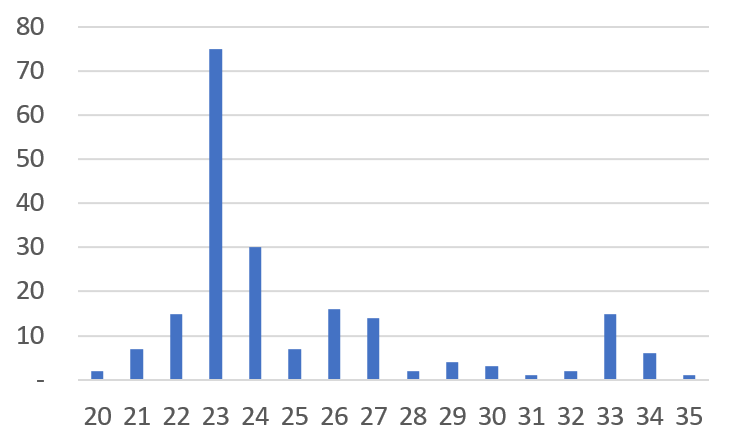
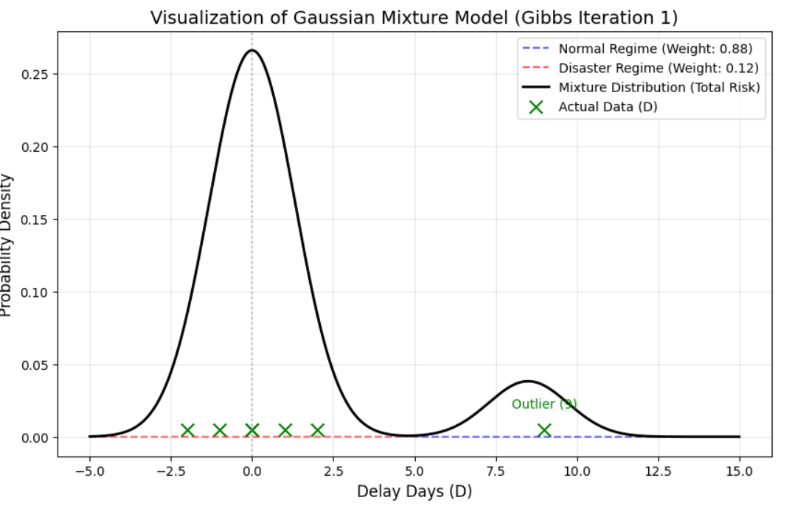
发现了有趣的相似性。我们的 Toy Data 以正常状态 (0) 为中心分散,同时形成了名为延迟状态 (9) 的另一个峰值。实际企业数据也区分为以平均 23 天这一正常 Lead Time 为中心的一个峰值,和以延迟状态 33 天为中心的(虽然微弱)另一个峰值。
大部分延迟天数 (Delay Days) 数据都会呈现出这种具有两个峰值的形态。在实际数据中,有时可能会出现 3 个以上的峰值。但是,我们不分别对数据的所有峰值进行建模,而是根据决策实际执行的结构(正常运营 vs 异常应对)将其压缩为 2-Regime (正常/延迟)。
这不仅仅是为了缩小现实。这是为了减少不确定性,稳定判断,并使执行具有一致性的 Operational Design 的侧面。细节模式(轻微延迟等)可以在需要时扩展,但基本引擎在定义为“正常”和“延迟”这两种状态 (Regime) 时最为坚固。
3. 统计假设:正态分布的合理性
在这里,我们建立一个重要的统计假设。“延迟天数数据服从以平均值为中心呈钟形分散的正态分布 (Normal Distribution)。”
为什么偏偏是正态分布?
有人可能会反问:“现实真的像教科书一样服从正态分布吗?”但是,根据统计学的中心极限定理 (Central Limit Theorem),各种独立变量(工人的状态、天气、交通状况、机械的微小误差等)合在一起出现的结果值,如果样本充足,将会收敛于正态分布。即,用正态分布对工序和物流的不确定性进行建模,在数学上成为最合理且合乎逻辑的方法。
4. 结论及下一步
最终我们看到的这个图表,是“正常状态的正态分布”和“延迟状态的正态分布”结合的样子。这正是小说中的 EXA 引擎想要解释的混合分布 (Mixture Distribution) 的实体。
[Part 1 的结论] 我们观测到的数据,即似然 (Likelihood) 函数是两个个别正态分布混合的混合分布。
第一阶段的目标是利用贝叶斯推断 (Bayesian Inference) 从由该混合分布组成的观测数据中找出 On-Time Risk,即可能发生延迟的概率。
为此,在下一篇文章 [附录 2] 中,将设计具体的数学模型,以便用贝叶斯方法解决由混合分布组成的似然函数。