意思決定インピーダンス整合 (Decision Impedance Matching)

BA02.[Exaベイズ推論] 営業の見えざる手：60日の賭けエピソードの去る第1部と第2部を通じて、私たちはベイズエンジンがどのように「事前信念」を立て、「シグナル」と「沈黙」を通じて確率の軌跡を追跡するかを見てきた。今、私たちの手にはベイズパラメータ α と β によって精巧に計算された純粋事後確率 P_raw が握られている。

しかし、まだ終わっていない。最後の意思決定過程が残っているからだ。60%の確率だとしても、それがたった一度のミーティングで得たものなのか、それとも数十回の交渉の末に導き出されたものなのかによって、決断の重みは完全に異なり得る。

残念ながら人間の脳は線形的な数字だけでは動かない。本日の付録第3部では、ベイズパラメータが持つ「証拠の総量」を通じて、冷徹な確率を決断の言語に変える「意思決定インピーダンス整合 (Decision Impedance Matching)」の秘密を探求してみる。

1. 数字の沼：なぜ51%は決断するのに不足なのか？

数学的に51%は半分を超えているので「成功の可能性が高い」ことを意味する。しかしビジネスの死活をかけた現場において、51%は事実上「一か八か」のギャンブルと変わらない。

ビジネス現場で最も危険なのは「根拠のない楽観」だ。

• 状況 A: α=0.6, β=0.4 (P=60%)
• 状況 B: α=60, β=40 (P=60%)

数学的確率 (P) は両方とも60%だ。しかしリーダーの立場からすると、状況Aは「運に任せるべきギャンブル」であり、状況Bは数多くの検証を経た結果（AとBの α, β の大きさが異なる。つまり、信念の大きさが違うのだ）である。前者は風一吹きでも0%や100%に乱高下しかねない不安定な状態だが、後者は並大抵の悪材料にも揺らがない「慣性」を持った状態だ。

人間の脳は単純に「比率」だけを見ない。その裏に敷かれた**「証拠の厚み」**を直感的に計算する。私たちはこの直感をシステムのロジックとして明示化する必要がある。

人間は不確実性を嫌悪し、特定の「臨界点 (Threshold)」を超えるまでは行動を留保する本性を持っている。反対に一度確信が立てば、85%の確率も95%の確率も同じく「確実」として受け入れる。

このように「数学的確率」と「心理的確信」の間には巨大な隔たりが存在する。電子工学において互いに異なる二つの回路を連結する際、エネルギー損失を減らすために抵抗値を合わせることを「インピーダンス整合」と言うように、システムの数字と人間の決断力を連結する精巧な調整が必要だ。

2. 証拠の総量 (n)：意思決定の臨界質量

BA02エピソードで適用されたExaのエンジンは、ベイズ事後確率（ここでは P_raw と表現）と証拠の総量 (n = α + β) を意思決定のフィルタとして使用する。これがまさに「意思決定インピーダンス整合」の核心だ。

2.1 信頼の体積と情報密度

ベイズパラメータ α と β はそれぞれ「成功の証拠」と「失敗の証拠」が積もった重さだ。この二つの和である n は、この案件について私たちが**「どれほど多く知っているか」**を表す指標となる。

• nが小さい時 (エネルギー不一致): システムの確率がいくら高くてもリーダーの確信には繋がらない。危険だからだ。これは回路のインピーダンスが合わずエネルギーが伝達されない状態だ。この時、エンジンは確率の代わりに「データ不足 (Not Enough Evidence)」という警告を送る。
• nが大きい時 (インピーダンス整合): 確率の数字がリーダーの決断力と共鳴し始める。十分な証拠が積もったので、もはや確率1%の変化は実際のビジネスリスクの1%の変化として精巧に伝達される。

これに対しエンジンは、組織の蓄積された総体的知識を込めて、人間の認知構造と類似した「シグモイド関数」を通過させ数字を練り直す。

2.2 シグモイド補正：確率に「意志」を込める

私たちは次のような非線形性を通じて確率の密度を調整する。

$$P_{calibrated} = \frac{1}{1 + e^{-k(P_{raw} – P_{0})}}$$

ここで P_raw はエンジンが計算したベイズの源泉事後確率であり、k は確信の傾き（確信の強度）、$P_0$ は意思決定の臨界点だ。

• 緩やかな区間 (不確実性): 確率が30〜50%の間にある時は補正値が非常に保守的に動く。「まだ信じるな」という信号だ。
• 急な区間 (決断): 確率が60%を超える瞬間、シグモイド曲線は急激に上がる。小さな肯定的シグナル一つが確率を60%から80%へと上昇させる。
• 飽和区間 (確信): 85%を超えれば曲線は再び緩やかになる。90%や95%も人間にとっては同一の**「Commit」**状態であることを反映するのだ。

今から意思決定インピーダンス整合に使われる核心概念ログオッズ (Log-odds) をオーバービューし、エンジン内部を数学的に暴いてみた後、最後にビジネスシミュレーションを通じてこれを理解してみよう。

3. 隠された世界：ログオッズ (Log-odds) の蓄積

Exaのベイズアップデートが起きるエンジン内部を覗いてみると、確率は私たちが知る0〜100%の姿ではない。ベイズのパラメータ α, β は数学的に「ログオッズ (Log-odds)」という無限の線形空間で作動する。

$$logit(P) = \ln\left(\frac{P}{1-P}\right) = \ln\left(\frac{\alpha}{\beta}\right)$$

私たちが営業ミーティング過程で新しいシグナルを得るたびに、システムはこのログオッズ値を正直に足していく。

• 交渉過程で捕捉した成功シグナルは +Δα を通じて値を押し上げ、
• 失敗シグナルと時間減衰 (λ) は +Δβ を通じて値を引き下げる。

この過程は電気回路で電荷が蓄積される過程と同じだ。しかしこのエネルギーはまだ「回路内部の電圧」に過ぎず、これを実際の機器を回す「動力」に変えるには外部抵抗と噛み合うインターフェースが必要だ。

3.1 シグモイド確率へのマッピング

なぜよりによってシグモイド関数なのか？ それはシグモイドがまさに上のログオッズ関数の逆関数 (Inverse Function) だからだ。無限の範囲 (-∞ ~ +∞) で積もった証拠の和を、私たちが理解できる0.0〜1.0の間の確率世界に戻す数学的唯一解だ。

$$P = \frac{1}{1 + e^{-k(x – x_0)}}$$

ここで x は私たちが積み上げてきたログオッズ (ln(α/β)) だ。この数式は単に数字を綺麗にするのではなく、無限の情報のエネルギーを有限の意思決定の範囲に圧縮する装置だ。

3.2 確率の世界 vs 情報の世界

私たちが住む世界は「確率 (Probability)」で対話するが、データが積もる原理は「情報の蓄積 (Information Accumulation)」だ。

• 確率の世界 (0〜1): この世界は非常に狭く息苦しい。0.9から0.99に行くのは難しく、1.0という壁に塞がれている。ここで数字を足したり引いたりすればすぐに壁にぶつかる。（例: 0.9 + 0.2 = 1.1 → 不可能）
• 情報の世界 (-∞ ~ +∞): この世界は終わりがない。証拠が積もれば積もるほど数字は無限に大きくなり得て、反対証拠が出れば無限に小さくなり得る。

ログオッズはまさにこの狭い確率の世界を広大な情報の世界へと広げた地図だ。

3.3 なぜログオッズがより妥当で説得力があるのか

① 証拠の「足し算」可能 (Additivity)

ベイズアップデートの核心は新しい情報が入ってくるたびに確率を修正することだ。確率空間ではこのために複雑な掛け算と割り算を繰り返さなければならないが、ログオッズ空間では単純な足し算になる。

「今日のミーティングは良かった (+2点)、しかし競合他社が現れた (-1.5点)」

このように私たちが直感的に点数をつけて足せる理由は、私たちの脳がすでに内部的にログオッズと類似した線形的な計算をしているからだ。

② 0と1という「壁」の除去

確率が99.9%の時と99.99999%の時、私たちは両方とも「ほぼ確実だ」と感じるが、その間には途方もない量の追加証拠が必要だ。ログオッズは1に近づくほど数字を幾何級数的に大きく広げることで、「確信が深まるほど、より多くの証拠が必要だ」というビジネス的真実を正確に描写する。

③ 対称性 (Symmetry)

成功確率が80%である状況と失敗確率が80%である状況（成功20%）はコインの裏表と同じだ。ログオッズ空間ではこの二つの状況が +1.38 と -1.38 として現れる。つまり、肯定と否定のエネルギーが鏡のように完璧な対称を成すことになり、ロジックの一貫性が確保される。

3.4 ベイズパラメータとの連結

α と β を使用してログオッズ (L) を表現すると次のようになる。

$$L = \ln\left(\frac{\alpha}{\beta}\right)$$

• 成功証拠 (α) が多くなれば L は陽数 (+) に大きくなる。
• 失敗証拠 (β) が多くなれば L は陰数 (-) に小さくなる。
• 両方の重さが同じなら L は 0 になる。（確率50%）

このようにログオッズは「誰の声がより大きいか？」を決める天秤の目盛りのようだ。ここまでがログオッズがなぜ「確率を無限の情報空間に広げて線形的に計算」する概念なのか、そしてビジネスロジックにおいて「より妥当な根拠」になるのかに対する大きな絵だ。

4. 数学的展開

もう少し気になる読者のために、Exaのエンジンで数学的にどのようにベイズのパラメータ (α, β) がログオッズという通路を経てシグモイド関数の指数部分に安着するようになるのか、その過程を段階別に見せたい。読む人によっては、この部分が最も興味深い時間になるかもしれない。

4.1 出発点：ベイズ事後確率 (P)

まず、私たちがアップデートした主人公 α と β を利用して計算された純粋確率 P を定義する。

$$P = \frac{\alpha}{\alpha + \beta}$$

この P 値は0と1の間を動き、私たちが直感的に理解する（事後）確率、すなわち勝率だ。

4.2 ログオッズ (Log-odds) への変換

今、この確率を無限の情報空間であるログオッズ (x) に広げる。ログオッズの定義に従って数式を展開すると驚くべき結果が出る。

$$x = \ln\left(\frac{P}{1-P}\right)$$

ここに上で定義した P 値を代入してみよう。

$$x = \ln\left(\frac{\frac{\alpha}{\alpha + \beta}}{1 – \frac{\alpha}{\alpha + \beta}}\right) = \ln\left(\frac{\frac{\alpha}{\alpha + \beta}}{\frac{\beta}{\alpha + \beta}}\right) = \ln\left(\frac{\alpha}{\beta}\right)$$

つまり、ログオッズ x は単純に成功証拠 (α) と失敗証拠 (β) の比率にログを取った値になる。これが情報の世界で私たちが積んだ「純粋な証拠の重さ」だ。

4.3 意思決定臨界点 (T) の変換

意思決定の臨界点 T もやはり確率単位（0.8など）だ。これをログオッズ空間の基準点である $x_0$ に変換する。

$$x_0 = \ln\left(\frac{T}{1-T}\right)$$

これで私たちは全てのデータを「ログオッズ」という同一の尺度の上で比較する準備ができた。

4.4 最終シグモイド結合 (インピーダンス整合)

さて最後にシグモイド関数の指数部分にこれら全ての値を入れる。シグモイド関数は指数部分に「現在のエネルギー ($x$) と基準エネルギー ($x_0$) の差」を受け入れる。

$$P_{out} = \frac{1}{1 + e^{-k(x – x_0)}}$$

この式に上で求めた x と $x_0$ を代入して指数部分を整理してみよう。

$$-k \left( \ln\frac{\alpha}{\beta} – \ln\frac{T}{1-T} \right) = -k \ln\left( \frac{\alpha / \beta}{T / (1-T)} \right)$$

したがって最終数式は次のように変貌する。

$$P_{out} = \frac{1}{1 + \left( \frac{\beta \cdot T}{\alpha(1-T)} \right)^k}$$

4.5 数学的結論とビジネス的意味

この展開がなぜ「臨界質量」と「説得力」を証明するのか要約してみよう。

1. 指数の魔法: 指数部分にあった複雑な e と ln が出会い互いに相殺され、結果的に成功比率 ($\frac{α}{β}$) と目標比率 ($\frac{T}{1-T)}$) の相対的大きさだけが残るようになる。
2. kの威力: k が指数の位置に位置するようになり、成功証拠が目標値を少し超えるだけでも確率を急激に増加させる。
3. データの重み反映: 単純に確率 (P) だけを見るのではなく、α と β という証拠の絶対量が大きくなるほど、この比率の力がより堅固になる。

5. ビジネスシミュレーション

実際のビジネスシナリオを通じて、この数学的モデルがどのように「決断のエネルギー」を作り出すのか証明してみせよう。

ある組織の性向に合わせてマスター基準値を次のように設定するとしよう。

• 意思決定臨界点 (T): 0.7 (70%)
  • 解釈：「少なくとも70%の確率的根拠はあってこそ勝負をかけてみる価値がある。」
• 決断加速度 (k): 10
  • 解釈：「臨界点を超えれば攻撃的にいく。」
• 最終数式:$$P_{out} = \frac{1}{1 + \left( \frac{\beta \cdot T}{\alpha(1-T)} \right)^k}$$

5.1 シミュレーションビジネスシナリオ

今、初期の信念（事前分布）が順次アップデートされた事後分布を持つ営業交渉過程のある段階を考える。下記の α と β は今まで交渉過程の Stage と Signal からベイズエンジンでアップデートされてきた α, β の値だ。

状況 1: 臨界点未達 (半信半疑の状態)

• データ: α=6.0, β=4.0 (純粋確率 P_raw = 60%)
• 計算過程:
  • 比率計算: $\frac{(4.0 * 0.7)}{(6.0 * 0.3)}$ ≈ 1.55
  • k乗適用: $1.55^{10}$ ≈ 81.3
  • 最終: $P_{out} = \frac{1}{(1 + 81.3)}$ ≈ 1.2%
• 解釈: ベイズ確率は60%だが、組織の基準 P_out (70%) に及ばない。システムは決断エネルギーを遮断し、意思決定権を持つ者に「まだ絶対信じるな (Hold)」という抑制信号を送る。

状況 2: 臨界点突破 (決断の始まり)

• データ: α=7.2, β=2.8 (純粋確率 P_raw = 72%)
• 計算過程:
  • 比率計算: $\frac{(2.8 * 0.7)}{(7.2 * 0.3)}$ ≈ 0.907
  • k乗適用: $0.907^{10}$ ≈ 0.38
  • 最終確率: $P_{out} = \frac{1}{(1 + 0.38) }$≈ 72.4%
• 解釈: 確率が臨界点 (T=0.7) を少し超えると、抑制されていたエネルギーが解かれ、純粋確率がそのままダッシュボードに反映され始める。「これからは関心を置いて見守る価値がある (Watch)」という信号だ。

状況 3: 臨界質量突破 (確信段階進入)

• データ: α=8.5, β=1.5 (純粋確率 P_raw = 85%)
• 計算過程:
  • 比率計算: $\frac{(1.5 * 0.7)} {(8.5 * 0.3)}$ ≈ 0.411
  • k乗適用: $0.411^{10}$ ≈ 0.0001
  • 最終確率: $P_{out} = \frac{1} {(1 + 0.0001)}$ ≈ 99.9%
• 解釈: 確率が85%に到達するや否や、加速度 k が魔法をかける。システムは85%という数字を「このプロジェクトはいける事業だ」という99.9%の確信 (Commit) へと押し上げる。リーダーはもはや躊躇する理由がない。

5.2 Insight

シナリオ各状況を要約して比較してみよう。

状態	純粋確率 (P_raw)	補正確率 (P_out)	意思決定等級	ビジネスアクション
未達	60%	1.2%	Hold	資源投入厳格禁止
突破	72%	72.4%	Push	戦略的集中開始
爆発	85%	99.9%	Commit	全社的資源集中

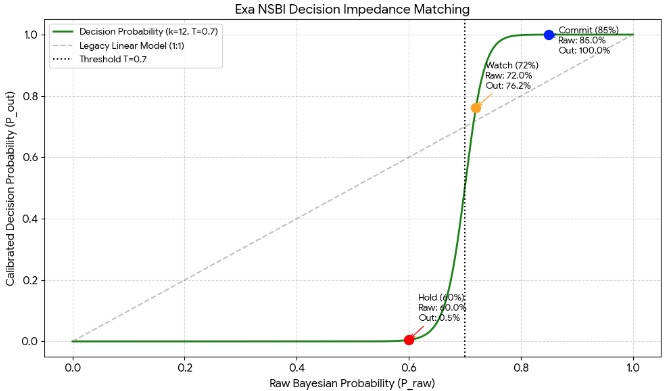
Insight: なぜこのモデルが勝利するのか – 営業意思決定のシステム化

1. 希望拷問の除去: 60%の確率を持つ案件を果敢に1%に底敷きしてしまうことで、営業現場の慢性的な弊害である「根拠のない楽観」をシステムが源泉遮断する。それにもかかわらず60%の事後確率は重要だ。したがってエンジンはベイズ確率と意思決定補正確率をダッシュボードに一緒に表示しなければならない。
2. ボトルネック資源の集中: 72%と85%はたった13%の差でしかないが、システムはこれを「関心」と「確信」という全く異なる次元に分離し出す。おかげで経営陣はどの事業に自分の時間を注ぐべきかを本能的に知るようになる。
3. インピーダンス整合の実体: この非線形的な跳躍こそが、ベテランリーダーたちが現場で感じる「勘が来た！」という心理的状態を数学的に完璧に複製したものだ。

ベイズエンジンの強力さはロジック自体だけでなく、それを組織の戦略、性格に合わせてチューニングできる柔軟性 (Flexibility) にある。