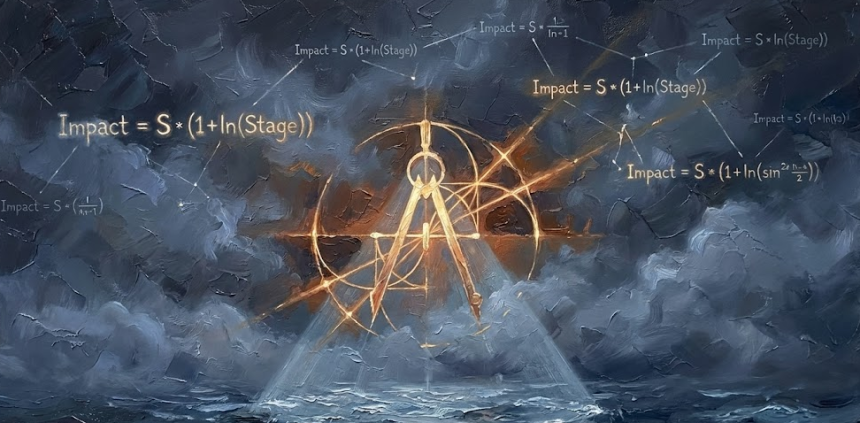尤度 (Likelihood)
この記事は [BA02. ベイズ推論] 営業の見えざる手:60日の賭けの第2部シリーズ記事である。前回の第1部「ベイズエンジン:不確実性を管理する数学的錬金術」では共役事前分布と解析解の優雅さを扱ったとすれば、第2部では証拠データである尤度(Likelihood)の計算と、ビジネス現場で最も脅威的な幽霊、「沈黙(Silence)」を数学的にどう処理するかを検討する。
この記事は単なる営業管理を超え、情報理論(Information Theory)と統計的重み付け設計がどのように結合して霧の中のリスクを可視化するか、その内面の作動原理についての物語である。
実際のビジネス現場、特に営業やSCM(サプライチェーン管理)の最前線は、教科書のようにデータが川の水のように流れる場所ではない。むしろそこは欠乏と断絶、そして「沈黙(Silence)」で満たされた空間だ。学習すべき(ビッグ)データは不足し、担当者たちは忙しくて入力を逃すのが常であり、システムは何日も放置されがちだ。
今日の2部では、このモデル(正規化された順次ベイズ推論:NSBI)の証拠データと「データの空白」さえも数学的リスクに翻訳し出すExaエンジンの設計美学を扱う。アラン・チューリングの統計的直感と情報理論を借りて、「データがなくても作動し、沈黙するほどスマートになるシステム」の数学的土台を公開する。
1. エントロピーの時間関数:沈黙は「0」ではない
ビジネスで最も危険な瞬間は、悪い知らせが聞こえてくる時ではない。むしろ「何の知らせもない期間」が長くなる時だ。これを無視して放置すれば、判断の誤りを犯すことになるだろう。
1.1 Time Kills All Deals:エントロピーの増加
情報理論(Information Theory)の観点から見ると、時間の流れの中で新しい情報が流入しないということは、それ自体がシステムのエントロピー(Entropy、無秩序度)が増加しているという強力な証拠だ。「便りがないのは良い便り」という格言は、ビジネスでは通用し難い。時間は全ての取引を殺す要素だからだ(Time Kills All Deals)。
我々のモデルは、この「沈黙の時間」を単なる空白にしておかない。代わりに数学的な「時間減衰(Time Decay)」ロジックを通じてリスクを計算する。
1.2 数学的実装:不確実性の拡張(分散の拡張)
実務現場で定義された時間内に記録が入力されなければ、時間が流れるたびにエンジン内部ではベイズ分布の失敗パラメータである β(ベータ)値を微細に増加させる。これは数学的に確率分布の分散(Variance)を強制的に広げる行為である。
これを数式で定義すると次の通りだ。
$$\beta_{t+1} = \beta_t + (\lambda \times \Delta t)$$
ここで λ(ラムダ)はリスク感度(Decay Factor)であり、Δt は沈黙した時間である。
解釈: 昨日まで受注確率が80%と堅固だったとしても、今日何の相互作用もなく一日(または一定期間)が過ぎれば、システムは明日の朝その確信を自ら蝕む。これはシステムが私たちに送る警告だ。「確信は放っておけば腐敗する」というビジネスの真理を数学的に実装したものだ。モデルはグラフを横に平べったく(Flat)し、沈黙を「現状維持」ではなく「信頼の摩耗」として解釈する。
2. 重さの幾何学:ヴェーバー・フェヒナーの法則
全く同じ「肯定的なシグナル」、例えば契約に対する意思決定権限を持つ役員がミーティングに参加したという事実が、全ての状況で同じ重さを持つだろうか? 最初の顔合わせ(第1段階)で決定権者に会うのと、最終契約直前(第5段階)で会うのとでは、後者の方がはるかに決定的であり破壊力が大きい。
私たちはこの微妙な「状況の文脈(Context)」をどうやって数字で統制できるだろうか? 単純に段階を1倍、2倍、3倍に増やす線形(Linear)方式は危険だ。システムが過度に単純になったり、後半であまりに敏感に反応して乱高下しかねないからだ。
2.1 対数重み付け(Logarithmic Weighting)
私たちはこのために認知心理学の「ヴェーバー・フェヒナーの法則(Weber-Fechner Law)」をモデルに適用する。「人間の感覚は刺激の強度に対して対数(Log)関数的に反応する」という原理だ。ビジネス段階の重要度もやはり幾何級数的に爆発するのではなく、対数曲線を描きながら重厚に増加するように反映するのが妥当だ。
これを反映した段階別重み(W)の数式は次の通りだ。
$$W = 1 + \ln(Stage)$$
ここで Stage は個別企業の現場状況を反映して定義した交渉(Meeting)段階の定義値だ。
この数式によれば、例えば探索段階(Stage 1)の重みは 1.0 (1+ln1) だが、交渉段階(Stage 5)の重みは約 2.61 (1+ln5) になる。つまり、この場合、終盤のシグナル一つが序盤のシグナルより2.6倍強力な「決定的な一発」として処理される。これは「終わるまで終わったわけではない」という現場の緊張感を数学的安定性(Stability)の中で実装し出した結果だ。
3. データがない場所に道を拓く:ヒューリスティック・モデリング
企業現場でデータサイエンスのために「学習させる(非定型な性格の)過去データが十分に存在する」事例は比較的稀だ。しかしこの状況でもモデルは光を放つ。ベイズ推論の強みは、データがない状況でも「合理的推論」が可能だという点にあるからだ。
私たちは不完全なデータを無理やり学習させる代わりに、ベテラン専門家たちの直感をモデルに移植する「ヒューリスティックスコアリング(Heuristic Scoring)」を選択する。
3.1 ヒューリスティックスコアテーブル(Heuristic Score Table)
第2次大戦当時、アラン・チューリングは少ない量の情報の欠片を集めてドイツ軍の暗号解読に成功した。彼は情報の量より「情報の質(Quality)」に注目し、これを証拠の重み(WoE)という概念として確立した。
我々のモデルはこの哲学を継承し、ビジネス現場で発生する数万種類の状況を核心的な信号に圧縮し、その「情報の密度」を専門家の視角で数値化する。「ヒューリスティックスコアテーブル」は統計ではなく、現場の経験と事前知識を反映した定義(Definition)だ。現場の固有性によって標準化できるだろうが、ここでは概略次のようなアイデアとして簡略に提示する。
- 決定的肯定(Strong Affirmation)シグナル:予算確定、役員同席など成功の兆候がはっきりした信号。
- 能動的否定(Active Resistance)シグナル:競合他社への言及、日程遅延など失敗の影が差した信号。
- 局面変化(Game Changer)シグナル:口頭承認のようなたった一つの信号だけでも全体の確率を覆せる強力なイベント。
各StageとSignalには固有のスコア値が配分される。収集されたSignalは性格によって肯定的(α)要因と否定的(β)要因に分類されベータ分布のパラメータに置換され、これはベイズロジックに従って直ちに事後分布の確率に反映される。このスコアテーブルはビッグデータ分析の結果物ではない。むしろ「決定権者が参加すれば実務者より2倍は確実だ」という現場の知恵を定数(Sscore)として凝縮し固定したものだ。
4. エンジンの心臓:直感と数学の結合(尤度:Likelihood)
さて、ベイズエンジン(Exa)の心臓でこれらの要素が計算過程でどのように一つに噛み合うのか見てみよう。
営業現場のシステム(Mobile, Tablet, Laptopなど)でミーティング段階(Stage)とミーティング結果として捕捉した信号(Signal)を入力する瞬間、システムはアップデート数式を稼動する。
$$\text{Update Value} = S_{score} \times W_{stage}$$
これを全体的なインパクト公式に拡張すれば、システムが計算する最終衝撃量は次のように導出される。
$$\text{Impact} = S_{signal} \times (1 + \ln(Stage))$$
これは前回の第1部で見てきた証拠データ(尤度、Likelihood)を計算する過程であり、これが事前分布と結合して事後分布の確率をアップデートすることになる。
軽さの中に込められた重さ
第2部の核心は、逆説的だが「システムの軽さ」にある。
私たちは高価なGPUサーバーや数年分のデータ精製プロジェクトなしでも、現場の経験や実務的知識など人間の直感が結合されたたった2枚のテーブル(Stage対数重み、Signalヒューリスティックスコア表)と数学的原理を結合し、最も現実的なエンタープライズ環境の推論エンジンを作り出すことができる。
時間減衰数式 βt+1 = βt + (λ × Δt) は私たちを怠惰な楽観論から目覚めさせ、
インパクト数式 Ssignal × (1 + ln(Stage)) は性急な判断を防ぎ決定的瞬間を捕捉する。
専門家のヒューリスティックはデータの空白と沈黙を知恵で満たす。
私たちはブラックボックスの中の魔法ではなく、説明可能で厳格な数学的論理の上に家を建てる。
[次回予告:第3部]
次回は冷徹な統計的確率(Raw Probability)を熱いビジネス意思決定に変える最後のパズル、「意思決定補正(Decision Calibration)とシグモイドの美学」について扱う番だ。