この記事は、小説形式で連載された「BA03 On-Time 資材入庫:Bayesian MCMC」編で活躍したEXAエンジンの作動原理を究明する技術解説シリーズの最初の記事です。
今回のシリーズは、ベイズ推論の中でも高級技法に属する混合分布(Mixture Distribution)とMCMC(Markov Chain Monte Carlo)Gibbs Samplingを扱うだけに、内容が深く計算過程が多少複雑になる可能性があります。したがって、これを可能な限り容易に消化できるよう段階別に分けて詳細にアプローチしたく、かなり長い旅程になることが予想されます。
全体的な脈絡の理解のために、小説の原文を先に一読することをお勧めします。併せて、ベイズ理論は段階的に概念が拡張されるため、BA01およびBA02のエピソードと数学解説を先に確認されれば、今回の内容を受け入れるのにはるかに役立つでしょう。これまでの数学的概念と論理が続くためです。
1. データの定義:観測偏差(Observation Deviation)
小説の中で扱う核心イシューである「On-Time(定時到着)」を数学的にモデリングするために、私たちはまずデータを定義しなければなりません。このために次のように日(Day)単位のサンプル観測データを生成します。
$$D = [d_1, d_2, \dots, d_7] = \{ -2, -1, 0, 1, 2, 0, 9 \}$$
私たちはこの観測された遅延日数の集合を一つのベクトル(Vector)として見ることができ、その中に含まれるそれぞれの遅延値($-2, -1, 0 \dots$)はこのベクトルを構成する要素(Element、または成分)となります。
ここで個別データ要素$d_i$は次のように定義されます。
$$d_i = (\text{実際の日付}) – (\text{計画された日付})$$
この数式が意味するところは非常に直感的です。
- :約束を正確に守った場合(On-Time)
- :計画より遅延した場合(例:+5は5日遅延)
- :計画より早く到着した場合(早期入庫)
このような遅延日数(Delay Days)モデルは、ビジネス現場の多様なボトルネック(Bottleneck)を測定するのに適用できます。
- 資材入庫および供給社の作業遅延(Lead Time Delay)
- 運送および物流遅延(Transportation Delay)
- 生産ラインの工程遅延(Production Delay)
ベクトルデータの大きさ(次元)はビジネス規模によって決定されます。観測された取引実績が100件なら100個の要素で、300件なら300個の要素で構成されたベクトルになるでしょう。
本シリーズではEXAエンジンの作動原理を明確に解剖して見せるために、先立って定義した7個の「トイデータ(Toy Data)」を例題として使用します。数百、数千件のデータは現実的ですが、複雑な計算過程を直感的に見せるには限界があるためです。
もちろん実際の現場に適用される時は、「供給先+品目+運送手段+到着地」または生産の「ライン+製品」など意思決定の目的に従ってデータを細分化(Granularity)して管理しなければならず、これを通じてSCM全般のリスクを正確に捕捉し出すことができます。
2. データの可視化:二つの峰
さて、今から私たちのToy Data(ベクトル)を可視化してみましょう。7個の要素がグラフ上にどのように配置されるか確認してみます。
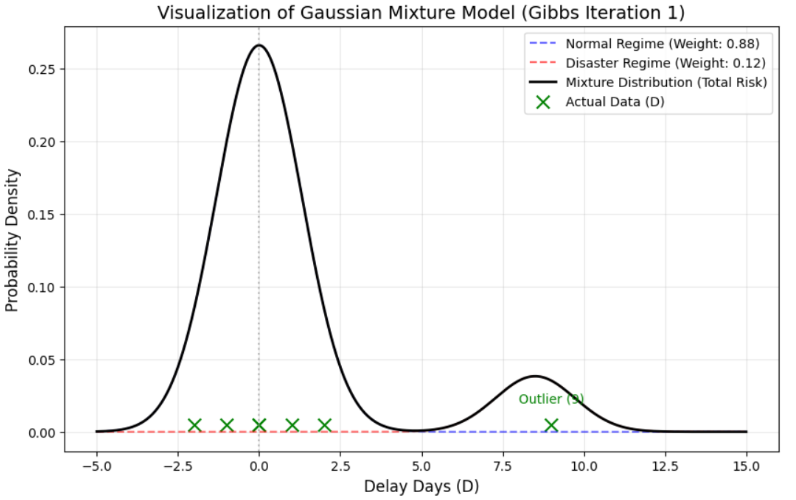
現実のデータはどうでしょうか? 下は実際の、ある企業の資材購買取引実績200件(特定供給社の特定品目)をヒストグラムで表したものです。
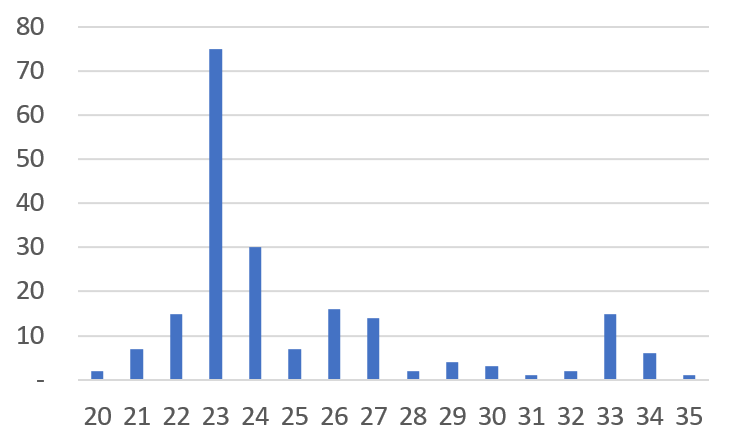
興味深い類似性が発見されます。私たちのToy Dataは正常状態(0)を中心に散らばっていながら、同時に遅延状態(9)という別途の峰を形成しています。実際の企業データもやはり正常リードタイムである平均23日を中心にした峰と、遅延状態である33日を中心にした(弱いですが)また別の峰に区分されます。
大部分の遅延日数(Delay Days)データはこのように二つの峰を持った形態を帯びるようになります。実際のデータには間々3個以上の峰が現れることもあります。しかし私たちはデータのすべての峰をそれぞれモデリングするより、意思決定が実際に実行される構造(正常運営 vs 非正常対応)に合わせて2-Regime(正常/遅延)に圧縮します。
これは現実を単純に縮小しようとするものではありません。不確実性を減らし判断を安定化させ、実行を一貫したものにするOperational Designの側面です。細部的なパターン(軽微な遅延など)は必要な時に拡張できますが、基本エンジンは「正常」と「遅延」という二つの状態(Regime)で定義する時が最も堅固です。
3. 統計的仮定:正規分布の妥当性
ここで私たちは重要な統計的仮定を一つ樹立します。「遅延日数データは平均を中心に鐘の形に散らばった正規分布(Normal Distribution)に従う。」
なぜよりによって正規分布なのか?
ある人は「現実が本当に教科書のように正規分布に従うのか?」と反問するかもしれません。しかし統計学の中心極限定理(Central Limit Theorem)によれば、様々な独立的な変数(作業者のコンディション、天気、交通状況、機械の微細な誤差など)が合わさって現れる結果値は、標本が十分な場合、正規分布に収束するようになります。すなわち、工程と物流の不確実性は正規分布でモデリングすることが数学的に最も妥当で合理的なアプローチになるためです。
4. 結論および次の段階
結局私たちが見ているこのグラフは、「正常状態の正規分布」と「遅延状態の正規分布」が合わさった姿です。これがまさに小説の中のEXAエンジンが解釈しようとする混合分布(Mixture Distribution)の実体です。
[Part 1の結論] 私たちが観測したデータ、すなわち尤度(Likelihood)関数は二つの個別正規分布が混合された混合分布です。
1次の目標はこの混合分布で構成された観測データからOn-Time Risk、すなわち遅延が発生する確率をベイズ推論(Bayesian Inference)で見つけ出すことです。
このために次の文[付録2]では、混合分布で構成された尤度関数をベイズで解決するための具体的な数学的モデルを設計します。