이 글은 소설 형식으로 연재된 ‘BA03 On-Time 자재입고: Bayesian MCMC‘ 편에서 활약한 EXA 엔진의 작동 원리를 규명하는 기술 해설 시리즈의 첫 번째 글입니다.
이번 시리즈는 베이지안 추론 중에서도 고급 기법에 속하는 혼합분포(Mixture Distribution)와 MCMC(Markov Chain Monte Carlo) Gibbs Sampling을 다루는 만큼, 내용이 깊고 계산 과정이 다소 복잡할 수 있습니다. 따라서 이를 가능한 쉽게 소화할 수 있도록 단계별로 나누어 상세히 접근하고자 하며, 제법 긴 여정이 될 것으로 예상됩니다.
전체적인 맥락 이해를 위해 소설 원문을 먼저 일독을 권합니다. 아울러 베이지안 이론은 단계적으로 개념이 확장되므로, BA01 및 BA02의 에피소드와 수학 해설을 먼저 살펴본다면 이번 내용을 받아들이는 데 훨씬 도움이 될 것입니다. 앞선 수학적 개념과 논리들이 이어지고 있습니다.
1. 데이터의 정의: 관측 편차 (Observation Deviation)
소설 속에서 다루는 핵심 이슈인 ‘On-Time(정시 도착)’을 수학적으로 모델링하기 위해, 우리는 가장 먼저 데이터를 정의해야 한다. 이를 위해 다음과 같이 일(Day) 단위의 샘플 관측 데이터를 생성한다.
$$D = [d_1, d_2, \dots, d_7] = { -2, -1, 0, 1, 2, 0, 9 }$$
우리는 이 관측된 지연 일수들의 집합 D를 하나의 벡터(Vector)로 볼 수 있으며, 그 안에 포함된 각각의 지연 값(-2, -1, 0 …)은 이 벡터를 구성하는 원소(Element, 또는 성분)가 된다.
여기서 개별 데이터 원소 는 다음과 같이 정의된다.
$$d_i = (\text{실제 일자}) – (\text{계획된 일자})$$
이 수식이 의미하는 바는 매우 직관적이다.
- : 약속을 정확히 지킨 경우 (On-Time)
- : 계획보다 지연된 경우 (예: +5는 5일 지연)
- : 계획보다 일찍 도착한 경우 (조기 입고)
이러한 지연 일수(Delay Days) 모델은 비즈니스 현장의 다양한 병목(Bottleneck)을 측정하는 데 적용될 수 있다.
- 자재 입고 및 공급사의 작업 지연 (Lead Time Delay)
- 운송 및 물류 지연 (Transportation Delay)
- 생산 라인의 공정 지연 (Production Delay)
벡터 데이터의 크기(차원)는 비즈니스 규모에 따라 결정된다. 관측된 거래 실적이 100건이라면 100개의 원소로, 300건이라면 300개의 원소로 구성된 벡터가 될 것이다.
본 시리즈에서는 EXA 엔진의 작동 원리를 명확하게 해부해 보이기 위해, 앞서 정의한 7개의 ‘장난감 데이터(Toy Data)’를 예제로 사용한다. 수백, 수천 건의 데이터는 현실적이지만, 복잡한 계산 과정을 직관적으로 보여주기에는 한계가 있기 때문이다.
물론 실제 현장에 적용될 때는 “공급처+품목+운송수단+도착지” 또는 생산의 “라인+제품” 등 의사결정 목적에 따라 데이터를 세분화(Granularity)하여 관리해야 하며, 이를 통해 SCM 전반의 리스크를 정확히 포착해 낼 수 있다.
2. 데이터의 시각화: 두 개의 봉우리
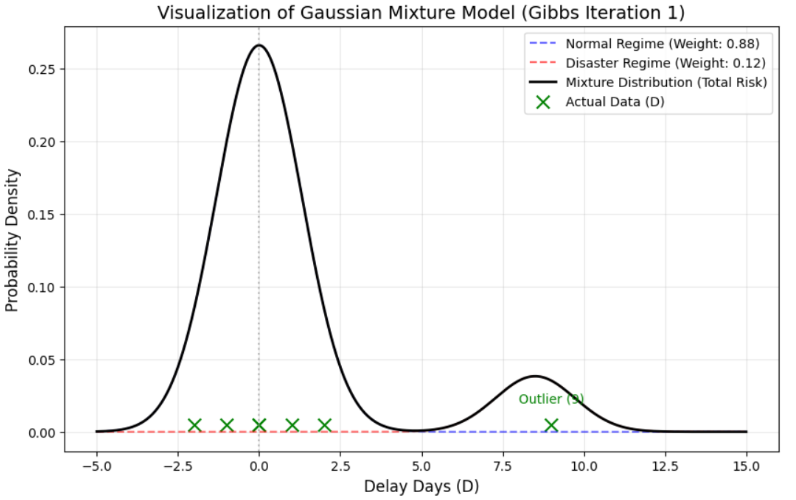
자, 이제 우리의 장난감 데이터(벡터 )를 시각화해 보자. 7개의 원소가 그래프 상에 어떻게 배치되는지 확인해 본다.
현실의 데이터는 어떨까? 아래는 실제 어느 기업의 자재 구매 거래 실적 200건(특정 공급사의 특정 품목)을 히스토그램으로 나타낸 것이다.
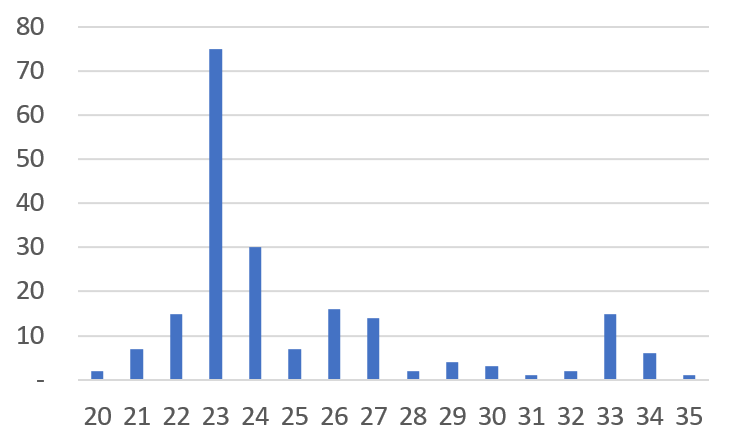
흥미로운 유사성이 발견된다. 우리의 장난감 데이터는 정상 상태(0)를 중심으로 흩어져 있으면서, 동시에 지연 상태(9)라는 별도의 봉우리를 형성하고 있다. 실제 기업 데이터 역시 정상 리드타임인 평균 23일을 중심으로 한 봉우리와, 지연 상태인 33일을 중심으로 약하지만 한 또 다른 봉우리로 구분된다.
대부분의 지연 일수 데이터는 이처럼 두 개의 봉우리를 가진 형태를 띄게 된다. 실제 데이터에는 간혹 3개 이상의 봉우리가 나타날 수도 있다. 그러나 우리는 데이터의 모든 봉우리를 각각 모델링하기보다, 의사결정이 실제로 실행되는 구조(정상 운영 vs 비정상 대응)에 맞춰 2-레짐(정상/지연)으로 압축한다.
이는 현실을 단순히 축소하려는 것이 아니다. 불확실성을 줄이고 판단을 안정화하며, 실행을 일관되게 만드는 운영 설계(Operational Design)의 측면이다. 세부적인 패턴(경미한 지연 등)은 필요할 때 확장할 수 있지만, 기본 엔진은 ‘정상’과 ‘지연’이라는 두 가지 상태(Regime)로 정의할 때 가장 견고하다.
3. 통계적 가정: 정규분포의 타당성
여기서 우리는 중요한 통계적 가정을 하나 수립한다. “지연 일수 데이터는 평균을 중심으로 종 모양으로 흩어진 정규분포(Normal Distribution)를 따른다.”
왜 하필 정규분포인가?
혹자는 “현실이 정말 교과서처럼 정규분포를 따르는가?”라고 반문할 수 있다. 하지만 통계학의 중심극한정리(Central Limit Theorem)에 따르면, 여러 독립적인 변수들(작업자의 컨디션, 날씨, 교통 상황, 기계의 미세한 오차 등)이 합쳐져서 나타나는 결과값은 표본이 충분할 경우 정규분포에 수렴하게 된다. 즉, 공정과 물류의 불확실성은 정규분포로 모델링하는 것이 수학적으로 가장 타당하고 합리적인 접근이 되기 때문이다.
4. 결론 및 다음 단계
결국 우리가 보고 있는 이 그래프는, ‘정상 상태의 정규분포’와 ‘지연 상태의 정규분포’가 합쳐진 모습이다. 이것이 바로 소설 속의 EXA 엔진이 해석하고자 하는 혼합 분포(Mixture Distribution)의 실체이다.
[Part 1의 결론] 우리가 관측한 데이터, 즉 우도(Likelihood) 함수는 두 개의 개별 정규분포가 혼합된 혼합분포이다.
1차 목표는 이 혼합분포로 구성된 관측 데이터로부터 On-Time Risk, 즉 지연이 발생할 수 있는 확률을 베이지안 추론으로 찾아내는 것이다.
이를 위해 다음 글 [부록2]에서는 혼합분포로 구성된 우도 함수를 베이지안으로 해결하기 위한 구체적인 수학적 모델을 설계한다.