Bài viết này là bài đầu tiên trong loạt bài giải thích kỹ thuật nhằm làm sáng tỏ nguyên lý hoạt động của động cơ EXA, vốn đóng vai trò quan trọng trong tập truyện dài kỳ định dạng tiểu thuyết ‘BA03 On-Time Nhập kho vật tư: Bayesian MCMC‘.
Vì loạt bài này đề cập đến Phân phối hỗn hợp (Mixture Distribution) và MCMC (Markov Chain Monte Carlo) Gibbs Sampling, thuộc các kỹ thuật cao cấp trong suy luận Bayesian, nên nội dung có thể sâu và quy trình tính toán hơi phức tạp. Do đó, để có thể tiếp thu điều này dễ dàng nhất có thể, chúng tôi dự định tiếp cận chi tiết bằng cách chia thành từng giai đoạn, và dự kiến đây sẽ là một hành trình khá dài.
Để hiểu bối cảnh tổng thể, chúng tôi khuyên bạn nên đọc tiểu thuyết gốc trước. Ngoài ra, vì lý thuyết Bayesian mở rộng khái niệm theo từng giai đoạn, nên nếu bạn xem trước các tập và giải thích toán học của BA01 và BA02, điều đó sẽ giúp ích rất nhiều cho việc tiếp nhận nội dung lần này. Bởi vì các khái niệm toán học và logic trước đó sẽ được tiếp nối.
1. Định nghĩa dữ liệu: Độ lệch quan sát (Observation Deviation)
Để mô hình hóa về mặt toán học vấn đề cốt lõi được đề cập trong tiểu thuyết là ‘On-Time (Đúng giờ)’, trước tiên chúng ta phải định nghĩa dữ liệu. Để làm điều này, chúng ta tạo dữ liệu quan sát mẫu theo đơn vị Ngày (Day) như sau:
Chúng ta có thể xem tập hợp các ngày trễ hạn được quan sát D này là một Vectơ (Vector), và mỗi giá trị trễ hạn (−2,−1,0…) bao gồm trong đó trở thành một Phần tử (Element, hoặc thành phần) cấu thành nên vectơ này.
Ở đây, phần tử dữ liệu riêng lẻ di được định nghĩa như sau:
Ý nghĩa của công thức này rất trực quan.
- di=0: Trường hợp giữ đúng hẹn chính xác (On-Time)
- di>0: Trường hợp trễ hơn kế hoạch (Ví dụ: +5 là trễ 5 ngày)
- di<0: Trường hợp đến sớm hơn kế hoạch (Nhập kho sớm)
Mô hình Số ngày trễ hạn (Delay Days) này có thể được áp dụng để đo lường các Nút thắt cổ chai (Bottleneck) đa dạng tại hiện trường kinh doanh.
- Nhập kho vật tư và sự chậm trễ trong công việc của nhà cung cấp (Lead Time Delay)
- Sự chậm trễ trong vận tải và logistics (Transportation Delay)
- Sự chậm trễ quy trình trong dây chuyền sản xuất (Production Delay)
Kích thước (chiều) của dữ liệu vectơ được quyết định theo quy mô kinh doanh. Nếu thành tích giao dịch được quan sát là 100 vụ, nó sẽ là một vectơ bao gồm 100 phần tử, nếu là 300 vụ, nó sẽ là vectơ bao gồm 300 phần tử.
Trong loạt bài này, để giải phẫu rõ ràng nguyên lý hoạt động của động cơ EXA, chúng tôi sử dụng 7 ‘Dữ liệu đồ chơi (Toy Data)’ đã định nghĩa ở trên làm ví dụ. Hàng trăm, hàng nghìn dữ liệu là thực tế, nhưng có giới hạn trong việc hiển thị trực quan các quy trình tính toán phức tạp.
Tất nhiên, khi áp dụng vào hiện trường thực tế, dữ liệu phải được quản lý bằng cách phân chia nhỏ (Granularity) tùy theo mục đích ra quyết định như “Nhà cung cấp + Mặt hàng + Phương tiện vận tải + Nơi đến” hoặc “Dây chuyền + Sản phẩm” trong sản xuất, và thông qua đó có thể nắm bắt chính xác rủi ro của toàn bộ SCM.
2. Trực quan hóa dữ liệu: Hai đỉnh
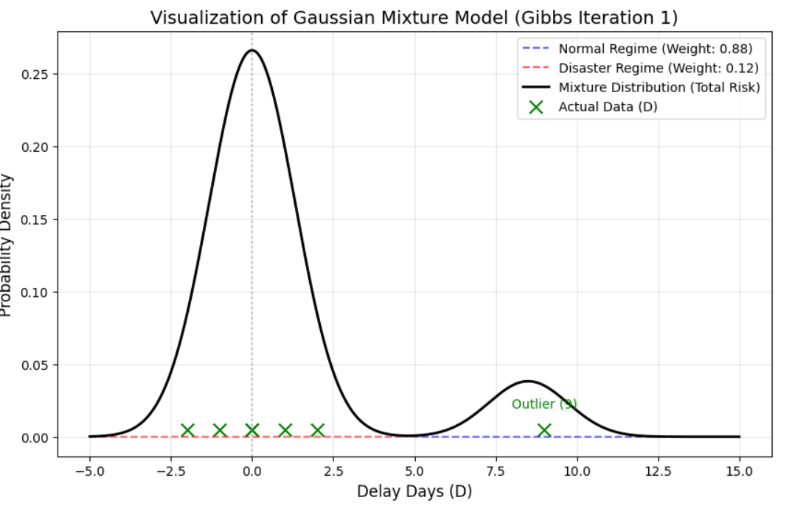
Nào, bây giờ hãy thử trực quan hóa Toy Data (Vectơ D) của chúng ta. Chúng ta hãy kiểm tra xem 7 phần tử được bố trí như thế nào trên biểu đồ.
Dữ liệu thực tế thì sao? Dưới đây là biểu đồ tần suất (histogram) thể hiện 200 thành tích giao dịch mua vật tư thực tế (mặt hàng cụ thể của nhà cung cấp cụ thể) của một doanh nghiệp nào đó.
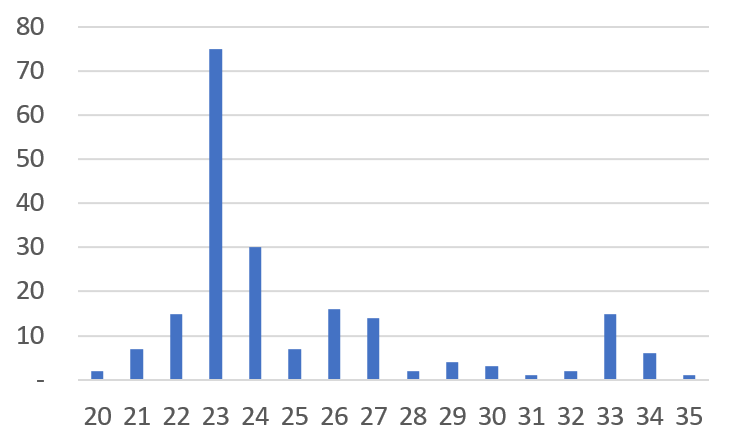
Một sự tương đồng thú vị được phát hiện. Toy Data của chúng ta nằm rải rác xung quanh trạng thái bình thường (0), đồng thời hình thành một đỉnh riêng biệt gọi là trạng thái trễ hạn (9). Dữ liệu doanh nghiệp thực tế cũng được phân chia thành một đỉnh lấy trung tâm là trung bình 23 ngày là Lead Time bình thường, và một đỉnh khác (tuy yếu hơn) lấy trung tâm là trạng thái trễ hạn 33 ngày.
Phần lớn dữ liệu Số ngày trễ hạn (Delay Days) sẽ mang hình thái có hai đỉnh như thế này. Trong dữ liệu thực tế, đôi khi có thể xuất hiện 3 đỉnh trở lên. Tuy nhiên, thay vì mô hình hóa từng đỉnh của dữ liệu, chúng tôi nén nó thành 2-Regime (Bình thường/Trễ hạn) để phù hợp với cấu trúc mà việc ra quyết định thực sự được thực hiện (Vận hành bình thường vs Ứng phó bất thường).
Điều này không đơn thuần là thu nhỏ thực tế. Đây là khía cạnh của Operational Design nhằm giảm thiểu sự không chắc chắn, ổn định phán đoán và làm cho việc thực thi trở nên nhất quán. Các mẫu chi tiết (như trễ hạn nhẹ, v.v.) có thể được mở rộng khi cần thiết, nhưng động cơ cơ bản vững chắc nhất khi được định nghĩa bằng hai trạng thái (Regime) là ‘Bình thường’ và ‘Trễ hạn’.
3. Giả định thống kê: Tính hợp lý của phân phối chuẩn
Tại đây, chúng tôi thiết lập một giả định thống kê quan trọng. “Dữ liệu số ngày trễ hạn tuân theo Phân phối chuẩn (Normal Distribution) nằm rải rác theo hình quả chuông xung quanh giá trị trung bình.”
Tại sao nhất định phải là Phân phối chuẩn?
Có người có thể hỏi ngược lại rằng “Thực tế có thực sự tuân theo phân phối chuẩn như sách giáo khoa không?” Tuy nhiên, theo Định lý giới hạn trung tâm (Central Limit Theorem) trong thống kê, giá trị kết quả xuất hiện khi nhiều biến số độc lập (tình trạng của công nhân, thời tiết, tình hình giao thông, sai số vi mô của máy móc, v.v.) hợp lại sẽ hội tụ về phân phối chuẩn nếu mẫu đủ lớn. Tức là, việc mô hình hóa sự không chắc chắn của quy trình và logistics bằng phân phối chuẩn trở thành cách tiếp cận hợp lý và thỏa đáng nhất về mặt toán học.
4. Kết luận và các bước tiếp theo
Cuối cùng, biểu đồ mà chúng ta đang xem này là hình dáng kết hợp của ‘Phân phối chuẩn của trạng thái bình thường’ và ‘Phân phối chuẩn của trạng thái trễ hạn’. Đây chính là thực thể của Phân phối hỗn hợp (Mixture Distribution) mà động cơ EXA trong tiểu thuyết muốn giải thích.
[Kết luận của Part 1] Dữ liệu chúng ta quan sát được, tức là hàm Thích hợp (Likelihood), là Phân phối hỗn hợp được trộn lẫn bởi hai phân phối chuẩn riêng biệt.
Mục tiêu giai đoạn 1 là tìm ra On-Time Risk, tức là xác suất có thể xảy ra trễ hạn, từ dữ liệu quan sát được cấu thành bởi phân phối hỗn hợp này bằng Suy luận Bayesian (Bayesian Inference).
Để làm điều này, trong bài viết tiếp theo [Phụ lục 2], chúng tôi sẽ thiết kế mô hình toán học cụ thể để giải quyết hàm Thích hợp được cấu thành bởi phân phối hỗn hợp bằng phương pháp Bayesian.