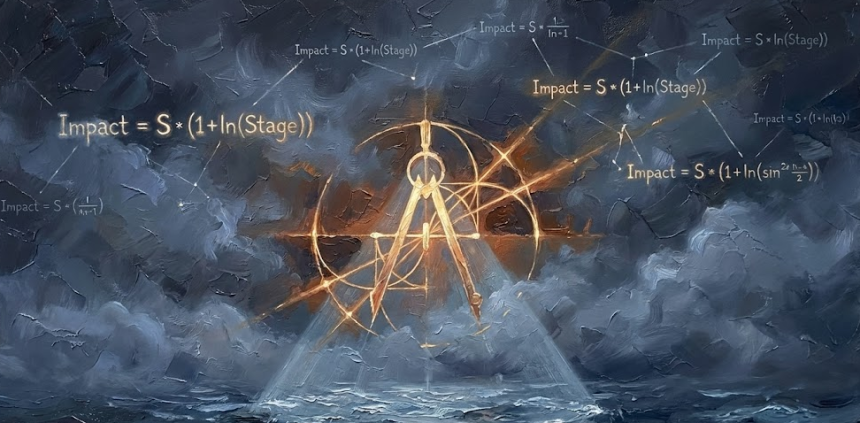Likelihood (Khả năng xảy ra)
Bài viết này là phần thứ 2 trong loạt bài về [BA02. Suy luận Bayesian] Bàn tay vô hình của kinh doanh: Canh bạc 60 ngày. Nếu như phần 1 “Động cơ Bayesian: Giả kim thuật toán học quản lý sự không chắc chắn” đã đề cập đến sự thanh lịch của phân phối tiên nghiệm liên hợp và giải pháp giải tích, thì phần 2 sẽ xem xét việc tính toán Likelihood (dữ liệu bằng chứng) và cách xử lý toán học đối với bóng ma đáng sợ nhất tại hiện trường kinh doanh, ‘Sự im lặng (Silence)’.
Bài viết này vượt ra ngoài việc quản lý kinh doanh đơn thuần, là câu chuyện về nguyên lý hoạt động bên trong của cách Lý thuyết Thông tin (Information Theory) và thiết kế trọng số thống kê kết hợp với nhau để trực quan hóa rủi ro trong màn sương mù.
Hiện trường kinh doanh thực tế, đặc biệt là tiền tuyến của bán hàng hay SCM (Quản lý chuỗi cung ứng), không phải là nơi dữ liệu chảy như sông giống trong sách giáo khoa. Ngược lại, đó là không gian tràn ngập sự thiếu hụt, đứt quãng và ‘Sự im lặng’. (Big) Data để học tập thì thiếu, người phụ trách bận rộn nên thường xuyên bỏ lỡ việc nhập liệu, và hệ thống thường bị bỏ mặc trong nhiều ngày.
Hôm nay trong phần 2, chúng ta sẽ đề cập đến thẩm mỹ thiết kế Động cơ Exa, thứ chuyển dịch dữ liệu bằng chứng của mô hình này (Suy luận Bayesian Tuần tự được Chuẩn hóa: NSBI) và thậm chí cả ‘khoảng trống dữ liệu’ thành rủi ro toán học. Mượn trực giác thống kê và lý thuyết thông tin của Alan Turing, chúng tôi xin công bố nền tảng toán học của “hệ thống hoạt động ngay cả khi không có dữ liệu và càng im lặng thì càng trở nên thông minh”.
1. Hàm thời gian của Entropy: Im lặng không phải là ‘0’
Khoảnh khắc nguy hiểm nhất trong kinh doanh không phải là khi nghe tin xấu. Mà là khi “khoảng thời gian không có tin tức gì” kéo dài. Nếu phớt lờ và bỏ mặc điều này, bạn sẽ phạm phải sai lầm trong phán đoán.
1.1 Time Kills All Deals: Sự gia tăng của Entropy
Dưới góc nhìn của Lý thuyết Thông tin, việc không có thông tin mới chảy vào theo dòng thời gian bản thân nó là bằng chứng mạnh mẽ cho thấy Entropy (Độ hỗn loạn) của hệ thống đang gia tăng. Câu châm ngôn “Không có tin tức là tin tốt” khó có thể áp dụng trong kinh doanh. Bởi vì thời gian là yếu tố giết chết mọi giao dịch (Time Kills All Deals).
Mô hình của chúng tôi không để ‘thời gian im lặng’ này là một khoảng trống đơn thuần. Thay vào đó, chúng tôi tính toán rủi ro thông qua logic toán học ‘Suy giảm theo thời gian (Time Decay)’.
1.2 Triển khai toán học: Mở rộng sự không chắc chắn (Mở rộng phương sai)
Nếu hồ sơ không được nhập trong thời gian quy định tại hiện trường thực tế, mỗi khi thời gian trôi qua, bên trong động cơ sẽ làm tăng vi mô giá trị β (Beta), tham số thất bại của phân phối Bayesian. Về mặt toán học, đây là hành vi cưỡng chế mở rộng Phương sai (Variance) của phân phối xác suất.
Điều này được định nghĩa bằng công thức sau:
$$\beta_{t+1} = \beta_t + (\lambda \times \Delta t)$$
Ở đây, λ (Lambda) là độ nhạy rủi ro (Decay Factor), và Δt là thời gian im lặng.
Diễn giải: Cho dù xác suất trúng thầu hôm qua vững chắc ở mức 80%, nhưng nếu hôm nay trôi qua một ngày (hoặc một khoảng thời gian nhất định) mà không có bất kỳ tương tác nào, hệ thống sẽ tự ăn mòn niềm tin đó vào sáng mai. Đây là lời cảnh báo mà hệ thống gửi cho chúng ta. Nó là sự triển khai toán học chân lý kinh doanh rằng “Niềm tin nếu để yên sẽ thối rữa”. Mô hình làm cho đồ thị trở nên bẹt ra (Flat) theo chiều ngang và diễn giải sự im lặng là ‘sự mài mòn của niềm tin’ chứ không phải là ‘duy trì hiện trạng’.
2. Hình học của trọng lượng: Định luật Weber-Fechner
Liệu cùng một “tín hiệu tích cực”, ví dụ như việc giám đốc có quyền ra quyết định hợp đồng tham gia cuộc họp, có mang cùng trọng lượng trong mọi tình huống không? Việc gặp người quyết định ở buổi gặp mặt đầu tiên (Giai đoạn 1) và gặp ngay trước khi ký hợp đồng cuối cùng (Giai đoạn 5), trường hợp sau mang tính quyết định và có sức công phá lớn hơn nhiều.
Làm thế nào chúng ta có thể kiểm soát ‘ngữ cảnh (Context) tình huống’ tinh tế này bằng các con số? Phương pháp tuyến tính (Linear) đơn thuần tăng giai đoạn lên 1 lần, 2 lần, 3 lần là rất nguy hiểm. Bởi vì hệ thống có thể trở nên quá đơn giản hoặc phản ứng quá nhạy cảm ở phần sau dẫn đến biến động mạnh.
2.1 Trọng số Logarit (Logarithmic Weighting)
Để làm điều này, chúng tôi áp dụng ‘Định luật Weber-Fechner’ của tâm lý học nhận thức vào mô hình. Đó là nguyên lý “Cảm giác của con người phản ứng theo hàm logarit (Log) đối với cường độ kích thích”. Tính hợp lý nằm ở việc phản ánh tầm quan trọng của giai đoạn kinh doanh không phải bùng nổ theo cấp số nhân, mà tăng lên một cách nặng ký theo đường cong logarit.
Công thức trọng số (W) theo giai đoạn phản ánh điều này như sau:
$$W = 1 + \ln(Stage)$$
Ở đây, Stage là giá trị định nghĩa giai đoạn đàm phán (Meeting) được xác định bằng cách phản ánh tình hình hiện trường của từng doanh nghiệp.
Theo công thức này, ví dụ trọng số của giai đoạn thăm dò (Stage 1) là 1.0 (1+ln1), nhưng trọng số của giai đoạn đàm phán (Stage 5) là khoảng 2.61 (1+ln5). Tức là, trong trường hợp này, một tín hiệu vào phút chót được xử lý như một ‘cú đánh quyết định’ mạnh gấp 2.6 lần tín hiệu ban đầu. Đây là kết quả của việc triển khai sự căng thẳng tại hiện trường rằng “Chưa kết thúc cho đến khi nó kết thúc” trong sự ổn định (Stability) toán học.
3. Mở đường nơi không có dữ liệu: Mô hình Heuristic
Tại hiện trường doanh nghiệp, trường hợp “tồn tại đủ dữ liệu quá khứ (tính chất phi cấu trúc) để huấn luyện” cho khoa học dữ liệu là tương đối hiếm. Nhưng ngay cả trong tình huống này, mô hình vẫn tỏa sáng. Bởi vì thế mạnh của suy luận Bayesian nằm ở chỗ có thể ‘suy luận hợp lý’ ngay cả trong tình huống không có dữ liệu.
Thay vì cưỡng ép huấn luyện dữ liệu không hoàn chỉnh, chúng tôi chọn ‘Chấm điểm Heuristic (Heuristic Scoring)’, cấy ghép trực giác của các chuyên gia kỳ cựu vào mô hình.
3.1 Bảng điểm Heuristic (Heuristic Score Table)
Trong Thế chiến II, Alan Turing đã thu thập những mảnh thông tin nhỏ và giải mã thành công mật mã của quân đội Đức. Ông chú ý đến ‘Chất lượng (Quality) thông tin’ hơn là lượng thông tin, và thiết lập nó thành khái niệm Trọng số Bằng chứng (WoE).
Mô hình của chúng tôi kế thừa triết lý này, nén hàng vạn tình huống phát sinh tại hiện trường kinh doanh thành các tín hiệu cốt lõi, và số hóa ‘mật độ thông tin’ đó dưới góc nhìn của chuyên gia. ‘Bảng điểm Heuristic’ không phải là thống kê mà là định nghĩa (Definition) phản ánh kinh nghiệm và kiến thức tiên nghiệm tại hiện trường. Tùy theo tính độc đáo của hiện trường mà có thể tiêu chuẩn hóa, nhưng ở đây tôi xin trình bày tóm tắt ý tưởng đại khái như sau.
- Tín hiệu Khẳng định Mạnh (Strong Affirmation): Các dấu hiệu thành công rõ ràng như xác định ngân sách, sự hiện diện của giám đốc.
- Tín hiệu Kháng cự Chủ động (Active Resistance): Các tín hiệu phủ bóng thất bại như đề cập đến đối thủ cạnh tranh, trì hoãn lịch trình.
- Tín hiệu Thay đổi Cuộc chơi (Game Changer): Sự kiện mạnh mẽ có thể đảo ngược toàn bộ xác suất chỉ với một tín hiệu duy nhất như phê duyệt miệng.
Mỗi Stage và Signal được phân bổ một giá trị điểm số riêng. Signal được thu thập sẽ được phân loại thành yếu tố tích cực (α) và tiêu cực (β) tùy theo tính chất để thay thế cho tham số của phân phối Beta, và điều này được phản ánh ngay lập tức vào xác suất của phân phối hậu nghiệm theo logic Bayesian. Bảng điểm này không phải là kết quả của phân tích Big Data. Ngược lại, nó là sự cô đọng và cố định trí tuệ hiện trường rằng “Nếu người quyết định tham gia thì chắc chắn gấp 2 lần so với người thực vụ” thành hằng số (S<sub>score</sub>).
4. Trái tim của động cơ: Sự kết hợp giữa Trực giác và Toán học (Likelihood)
Bây giờ hãy xem các yếu tố này khớp với nhau như thế nào trong quá trình tính toán tại trái tim của Động cơ Bayesian (Exa).
Khoảnh khắc nhập giai đoạn cuộc họp (Stage) và tín hiệu (Signal) thu được từ kết quả cuộc họp trên hệ thống hiện trường kinh doanh (Mobile, Tablet, Laptop, v.v.), hệ thống sẽ khởi động công thức cập nhật.
$$\text{Update Value} = S_{score} \times W_{stage}$$
Mở rộng điều này thành công thức tác động tổng thể, lượng xung kích cuối cùng mà hệ thống tính toán được rút ra như sau:
$$\text{Impact} = S_{signal} \times (1 + \ln(Stage))$$
Đây là quá trình tính toán dữ liệu bằng chứng (Likelihood) mà chúng ta đã xem xét ở phần 1, và nó kết hợp với phân phối tiên nghiệm để cập nhật xác suất phân phối hậu nghiệm.
Sự nặng nề chứa đựng trong sự nhẹ nhàng
Cốt lõi của phần 2, nghịch lý thay, lại nằm ở ‘sự nhẹ nhàng của hệ thống’.
Chúng ta không cần máy chủ GPU đắt tiền hay dự án làm sạch dữ liệu kéo dài nhiều năm, mà chỉ cần kết hợp nguyên lý toán học với hai bảng duy nhất (Trọng số log Stage, Bảng điểm Heuristic Signal) kết hợp trực giác con người như kinh nghiệm hiện trường và kiến thức thực vụ, để tạo ra động cơ suy luận môi trường doanh nghiệp thực tế nhất.
Công thức suy giảm theo thời gian βt+1 = βt + (λ × Δt) đánh thức chúng ta khỏi sự lạc quan lười biếng,
Công thức tác động Ssignal × (1 + ln(Stage)) ngăn chặn phán đoán vội vàng và nắm bắt khoảnh khắc quyết định.
Heuristic chuyên gia lấp đầy khoảng trống dữ liệu và sự im lặng bằng trí tuệ.
Chúng tôi không xây nhà trên ma thuật trong hộp đen, mà trên logic toán học nghiêm ngặt và có thể giải thích được.
[Teaser Tiếp theo: Phần 3]
Lần tới sẽ đến lượt mảnh ghép cuối cùng biến xác suất thống kê lạnh lùng (Raw Probability) thành quyết định kinh doanh nóng hổi, ‘Hiệu chỉnh Ra quyết định (Decision Calibration) và Thẩm mỹ của Sigmoid’.