BA02.[附录 3] 销售成功概率决策支持系统

决策阻抗匹配 (Decision Impedance Matching)

通过 BA02.[Exa 贝叶斯推断] 销售的一双看不见的手：60 天赌局插曲的上一篇第一部和第二部，我们探讨了贝叶斯引擎如何建立“先验信念”，并通过“信号”和“沉默”追踪概率的轨迹。现在，我们手中握着由贝叶斯参数 α 和 β 精密计算出的纯后验概率 P_raw。

但这还没有结束。因为还有最后的决策过程。即使是 60% 的概率，根据它是通过一次会议获得的，还是经过数十次谈判得出的，决断的分量可能会截然不同。

遗憾的是，人类的大脑并不仅仅依靠线性的数字运作。在今天的附录第三部中，我们将探索“决策阻抗匹配 (Decision Impedance Matching)”的秘密，通过贝叶斯参数所拥有的“证据总量”，将冷静的概率转化为决断的语言。

1. 数字的沼泽：为什么 51% 不足以做出决断？

在数学上，51% 超过了一半，因此意味着“成功的可能性很高”。但在决一死战的商业现场，51% 实际上与“孤注一掷”的赌博无异。

商业现场最危险的是**“毫无根据的乐观”**。

• 情况 A: α=0.6, β=0.4 (P=60%)
• 情况 B: α=60, β=40 (P=60%)

数学概率 (P) 两者都是 60%。但在领导者的立场上，情况 A 是“必须听天由命的赌博”，而情况 B 是经过无数次验证的结果（A 和 B 的 α, β 大小不同。即，信念的大小不同）。前者是连一阵微风都能使其在 0% 或 100% 之间剧烈波动的动荡状态，而后者是拥有即使遇到一般的利空消息也不会动摇的“惯性”的状态。

人类的大脑不只是单纯地看“比率”。它会直观地计算其背后铺垫的“证据的厚度”。我们需要将这种直觉明示为系统的逻辑。

人类厌恶不确定性，并且拥有在跨过特定“临界点 (Threshold)”之前保留行动的本性。相反，一旦确信，就会将 85% 的概率或 95% 的概率同样作为“确定”来接受。

像这样，在**“数学概率”和“心理确信”**之间存在着巨大的鸿沟。就像在电子工程中连接两个不同的电路时，为了减少能量损失而匹配电阻值称为“阻抗匹配”一样，需要连接系统的数字和人类决断力的精密协调。

2. 证据总量 (n)：决策的临界质量

在 BA02 插曲中应用的 Exa 引擎，使用贝叶斯后验概率（这里表示为 P_raw）和证据总量 (n = α + β) 作为决策的过滤器。这正是“决策阻抗匹配”的核心。

2.1 信任的体积与信息密度

贝叶斯参数 α 和 β 分别是“成功的证据”和“失败的证据”积累的重量。两者的总和 n 成为表示我们对这笔交易“知道多少”的指标。

• 当 n 很小时 (能量不匹配): 无论系统的概率多高，都不会导致领导者的确信。因为很危险。这是电路阻抗不匹配导致能量无法传递的状态。此时，引擎会发出“数据不足 (Not Enough Evidence)”的警告，而不是概率。
• 当 n 很大时 (阻抗匹配): 概率数字开始与领导者的决断力产生共鸣。因为积累了充足的证据，现在 1% 的概率变化会作为实际商业风险的 1% 变化被精密地传递。

对此，引擎包含组织积累的总体知识，并通过与人类认知结构类似的“S 型 (Sigmoid) 函数”重新塑造数字。

2.2 S 型校准：在概率中注入“意志”

我们通过如下的非线性调整概率的密度。

$$P_{calibrated} = \frac{1}{1 + e^{-k(P_{raw} – P_{0})}}$$

这里 $P_{raw}$ 是引擎计算的贝叶斯源后验概率，k 是确信的斜率（确信的强度），$P_0$ 是决策的临界点。

• 平缓区间 (不确定性): 概率在 30~50% 之间时，校准值的变动非常保守。这是**“还不要相信”**的信号。
• 陡峭区间 (决断): 概率超过 60% 的瞬间，S 型曲线急剧上升。一个小的积极信号就能将概率从 60% 提升到 80%。
• 饱和区间 (确信): 超过 85% 后，曲线再次变得平缓。这反映了 90% 或 95% 对人类来说都是相同的“Commit”状态。

从现在起，让我们概览用于决策阻抗匹配的核心概念对数几率 (Log-odds)，并在数学上剖析引擎内部，最后通过商业模拟来理解这一点。

3. 隐藏的世界：对数几率 (Log-odds) 的积累

窥探 Exa 的贝叶斯更新发生的引擎内部，概率并非我们所知的 0~100% 的样子。贝叶斯的参数 α, β 在数学上在名为“对数几率 (Log-odds)”的无限线性空间中运作。

$$logit(P) = \ln\left(\frac{P}{1-P}\right) = \ln\left(\frac{\alpha}{\beta}\right)$$

每当我们在销售会议过程中获得新信号时，系统都会诚实地加上这个对数几率值。

• 在谈判过程中捕捉到的成功信号通过 +Δα 推高数值，
• 失败信号和时间衰减 (λ) 通过 +Δβ 拉低数值。

这个过程就像电路中电荷积累的过程。但这股能量还只是“电路内部的电压”，要将其转化为驱动实际设备的“动力”，需要与外部电阻啮合的接口。

3.1 映射到 S 型概率

为什么偏偏是 S 型函数？因为 S 型正是上面对数几率函数的反函数 (Inverse Function)。它是将无限范围 (-∞ ~ +∞) 内积累的证据之和返回到我们可以理解的 0.0 ~ 1.0 之间概率世界的数学唯一解。

$$P = \frac{1}{1 + e^{-k(x – x_0)}}$$

这里 x 是我们积累的对数几率 (ln(α/β))。这个公式不仅仅是让数字变漂亮的装置，而是将无限信息的能量压缩到有限决策范围的装置。

3.2 概率的世界 vs 信息的世界

我们生活的世界用“概率 (Probability)”对话，但数据积累的原理是“信息的积累 (Information Accumulation)”。

• 概率的世界 (0 ~ 1): 这个世界非常狭窄且郁闷。很难从 0.9 走到 0.99，且被 1.0 的墙壁挡住。在这里加减数字很快就会撞墙。（例如：0.9 + 0.2 = 1.1 → 不可能）
• 信息的世界 (-∞ ~ +∞): 这个世界没有尽头。证据越积累数字可以变得无限大，如果出现相反证据可以变得无限小。

对数几率正是将这个狭窄的概率世界展开为广阔的信息世界的地图。

3.3 为什么对数几率更合理且更有说服力

① 证据的“可加性” (Additivity)

贝叶斯更新的核心是每当新信息进入时修正概率。在概率空间中，为此必须重复复杂的乘法和除法，但在对数几率空间中，这变成了单纯的加法。

“今天的会议很好 (+2 分)，但竞争对手出现了 (-1.5 分)”

我们之所以能像这样直观地打分并相加，是因为我们的大脑已经在内部进行着与对数几率类似的线性计算。

② 去除 0 和 1 的“墙”

概率为 99.9% 时和 99.99999% 时，我们都感觉“几乎确定”，但这之间需要巨量的额外证据。对数几率通过越接近 1 就以几何级数大幅展开数字，准确地描绘了**“确信越深，需要越多证据”**的商业真理。

③ 对称性 (Symmetry)

成功概率为 80% 的情况和失败概率为 80% 的情况（成功 20%）就像硬币的两面。在对数几率空间中，这两种情况表现为 +1.38 和 -1.38。即，肯定和否定的能量像镜子一样形成完美的对称，确保了逻辑的一致性。

3.4 与贝叶斯参数的连接

使用 α 和 β 表达对数几率 (L) 如下：

$$L = \ln\left(\frac{\alpha}{\beta}\right)$$

• 如果成功证据 (α) 变多，L 向正数 (+) 变大。
• 如果失败证据 (β) 变多，L 向负数 (-) 变小。
• 如果两者的重量相同，L 变为 0。（概率 50%）

像这样，对数几率就像决定“谁的声音更大？”的天平刻度。到此为止是关于为什么对数几率是“将概率展开到无限信息空间进行线性计算”的概念，以及为何在商业逻辑中成为“更合理的依据”的大图景。

4. 数学展开

为了更好奇的读者，我想分阶段展示在 Exa 的引擎中，贝叶斯的参数 (α, β) 在数学上是如何经过对数几率这个通道，安顿在 S 型函数的指数部分的。根据读者的不同，这部分可能是最有趣的时光。

4.1 出发点：贝叶斯后验概率 (P)

首先，定义利用我们更新的主人公 α 和 β 计算出的纯概率 P。

$$P = \frac{\alpha}{\alpha + \beta}$$

这个 P 值在 0 和 1 之间移动，是我们直观理解的（后验）概率，即胜率。

4.2 转换为对数几率 (Log-odds)

现在，将此概率展开到无限信息空间——对数几率 (x)。根据对数几率的定义展开公式，会出现惊人的结果。

$$x = \ln\left(\frac{P}{1-P}\right)$$

试着将上面定义的 P 值代入这里。

$$x = \ln\left(\frac{\frac{\alpha}{\alpha + \beta}}{1 – \frac{\alpha}{\alpha + \beta}}\right) = \ln\left(\frac{\frac{\alpha}{\alpha + \beta}}{\frac{\beta}{\alpha + \beta}}\right) = \ln\left(\frac{\alpha}{\beta}\right)$$

即，对数几率 x 变成了单纯地对成功证据 (α) 和失败证据 (β) 的比率取对数的值。这是我们在信息世界中积累的“纯粹的证据重量”。

4.3 决策临界点 (T) 的转换

决策临界点 T 也是概率单位（0.8 等）。将其转换为对数几率空间的基准点 $x_0$。

$$x_0 = \ln\left(\frac{T}{1-T}\right)$$

现在我们准备好在名为“对数几率”的同一尺度上比较所有数据了。

4.4 最终 S 型结合 (阻抗匹配)

现在最后将所有这些值放入 S 型函数的指数部分。S 型函数在指数部分接受**“当前能量 ($x$) 和基准能量 ($x_0$) 的差”**。

$$P_{out} = \frac{1}{1 + e^{-k(x – x_0)}}$$

将上面求出的 $x$ 和 $x_0$ 代入此式，整理指数部分。

$$-k \left( \ln\frac{\alpha}{\beta} – \ln\frac{T}{1-T} \right) = -k \ln\left( \frac{\alpha / \beta}{T / (1-T)} \right)$$

因此最终公式变形如下。

$$P_{out} = \frac{1}{1 + \left( \frac{\beta \cdot T}{\alpha(1-T)} \right)^k}$$

4.5 数学结论与商业意义

让我们总结一下为什么这一展开证明了“临界质量”和“说服力”。

1. 指数的魔法: 指数部分复杂的 e 和 ln 相遇并互相抵消，结果只剩下成功比率 ($\frac{α}{β}$) 和目标比率 ($\frac{T}{(1-T)}$) 的相对大小。
2. k 的威力: 随着 k 位于指数位置，成功证据哪怕只稍微超过目标值，也会使概率急剧增加。
3. 反映数据的重量: 不仅仅是单纯地看概率 (P)，随着名为 α 和 β 的证据绝对量变大，这个比率的力量会变得更加坚固。

5. 商业模拟

让我们通过实际的商业场景来证明这个数学模型是如何创造“决断的能量”的。

假设根据某组织的倾向如下设定主基准值。

• 决策临界点 (T): 0.7 (70%)
  • 解释：“至少要有 70% 的概率依据才值得一搏。”
• 决断加速度 (k): 10
  • 解释：“如果超过临界点就积极行动。”
• 最终公式:$$P_{out} = \frac{1}{1 + \left( \frac{\beta \cdot T}{\alpha(1-T)} \right)^k}$$

5.1 模拟商业场景

现在，思考拥有从初始信念（先验分布）顺次更新的后验分布的销售谈判过程的某个阶段。下面的 α 和 β 是从至今为止谈判过程的 Stage 和 Signal 在贝叶斯引擎中更新的 α, β 值。

情况 1: 未达临界点 (半信半疑的状态)

• 数据: α=6.0, β=4.0 (纯概率 $P_{raw}$ = 60%)
• 计算过程:
  • 比率计算: $\frac{(4.0 * 0.7)}{(6.0 * 0.3)}$ ≈ 1.55
  • 应用 k 次方: $1.55^{10}$ ≈ 81.3
  • 最终: $P_{out} = \frac{1}{(1 + 81.3)}$ ≈ 1.2%
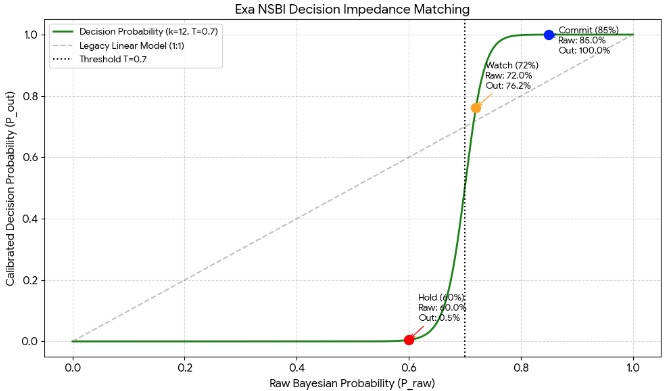
• 解释: 贝叶斯概率是 60%，但未达到组织的标准 $P_{out}$ (70%)。系统切断决断能量，向拥有决策权的人发送“还绝对不要相信 (Hold)”的抑制信号。

情况 2: 突破临界点 (决断的开始)

• 数据: α=7.2, β=2.8 (纯概率 $P_{raw}$ = 72%)
• 计算过程:
  • 比率计算: $\frac{(2.8 * 0.7)}{(7.2 * 0.3)}$ ≈ 0.907
  • 应用 k 次方: $0.907^{10}$ ≈ 0.38
  • 最终概率: $P_{out} = \frac{1}{(1 + 0.38)}$ ≈ 72.4%
• 解释: 概率刚稍微超过临界点 (T=0.7)，被抑制的能量释放，纯概率开始原样反映在仪表板上。这是“从现在起值得关注 (Watch)”的信号。

情况 3: 突破临界质量 (进入确信阶段)

• 数据: α=8.5, β=1.5 (纯概率 $P_{raw}$ = 85%)
• 计算过程:
  • 比率计算: $\frac{(1.5 * 0.7)}{(8.5 * 0.3)}$ ≈ 0.411
  • $0.411^{10}$应用 k 次方: 0.411^10 ≈ 0.0001
  • 最终概率: $P_{out} = \frac{1}{(1 + 0.0001)}$ ≈ 99.9%
• 解释: 概率一达到 85%，加速度 k 就施展魔法。系统将 85% 这个数字推高到“这个项目是能成的生意”的 99.9% 确信 (Commit)。领导者再也没有理由犹豫。

5.2 Insight

让我们总结并比较场景的各种情况。

状态	纯概率 (P_raw)	校准概率 (P_out)	决策等级	商业行动
未达	60%	1.2%	Hold	严禁投入资源
突破	72%	72.4%	Push	开始战略集中
爆发	85%	99.9%	Commit	集中全公司资源

Insight: 为什么这个模型会胜利 – 销售决策的系统化

1. 消除希望拷问: 通过果断地将拥有 60% 概率的交易压低到 1%，系统从源头上阻断了作为销售现场痼疾的“毫无根据的乐观”。即便如此，60% 的后验概率依然重要。因此引擎必须在仪表板上同时显示贝叶斯概率和决策校准概率。
2. 瓶颈资源的集中: 72% 和 85% 虽然只有 13% 的差距，但系统将其分离为“关注”和“确信”这两个完全不同的维度。得益于此，管理层本能地知道应该把我的时间投入到哪个业务中。
3. 阻抗匹配的实体: 这种非线性的飞跃正是数学上完美复制了资深领导者在现场感觉到的“有感觉了！”的心理状态。

贝叶斯引擎的强大不仅在于逻辑本身，还在于能够根据组织的战略、性格进行调整的灵活性 (Flexibility)。